vol. 16 no. 3, September, 2011
vol. 16 no. 3, September, 2011 |
||||
In this paper, we report on motifs that take the form of interaction patterns in serendipity. Our study of motifs was one aspect of a larger research project employing network methods to describe and measure social structure and process in serendipity. Four dominant motifs were detected, each displaying distinct interaction and attribute patterning. The motif findings have theoretical implications, providing evidence for the concept of normative interaction patterns in serendipity and supporting ideas relating to the importance of people and information in serendipity.
A motif is a recurring theme, sub-structure, pattern or idea appearing within the bounds of a larger structure. In some contexts, for example, in works of music, art, narrative, and architecture, motifs are considered to inform, develop, and support the larger structured work. Motifs in such contexts are rarely viewed as objective or neutral, but rather as fundamental building blocks without which the work would be less effective and have less impact. In network contexts, motifs are defined more formally as sub-networks that occur with statistically significant frequency. It is important to note that in this context, statistical frequency does not automatically equate with the non-statistical concept of importance (Milo et al. 2002).
Motif detection has been applied most extensively in the field of bioinformatics, where the technique has been used to identify recurring sub-structures in protein sequences and gene regulatory sequences (for example, see http://meme.sdsc.edu/meme/meme-intro.html ). Motif detection has also been employed in information-related network research, including the study of email networks, blogs and comment networks, and the Web (Juszczyszyn and Musial 2011; Kamaliha et al. 2008; Kolaczyk 2009; Qazvinian et al. n.d.; Milo et al. 2002). Motifs help to characterise or classify the larger structure in which they occur (Gao et al. 1999) and can even define and predict the larger structure's global topology (Vázquez et al. 2004). Once detected, motifs are used for theoretical purposes, especially for modelling and simulation.
Introduced in 1754 in a letter to a friend by the British 'correspondent extraordinaire', Henry Walpole, as '... making discoveries, by accidents and sagacity, of things which [one is] not in quest of..'. ( Remer 1965: 16; Walpole in Merton and Barber 2004: 2), and elaborated, unfortunately, with a rather inept accompanying explanation, the word serendipity has been problematic ever since it entered common usage in the late nineteenth century, subjected to many redefinitions, various classification attempts, and extensive changes in semantic use (Remer 1965; Merton and Barber 2004). Irrespective of uncertainties concerning the precision and/or vagueness of its meaning, serendipity has always retained the concept of duality at its core. Our accepted understanding of the phenomenon requires the internal (e.g. the prepared mind) and the external (e.g. outside context and events) to come together in the right way, with neither on its own considered enough for the classification of an experience as serendipity.
Several attributes bind the nature of serendipity. Lived, personal and experiential, serendipity is fundamentally phenomenological. Sociologically, we recognise serendipity as a normative phenomenon yet accept that what may be serendipity for one person may not be for another. Although sometimes described as a sudden moment of recognition, the clichéd flash of inspiration, serendipity is, upon closer inspection, both longitudinal and cumulative, the result of multiple events occurring over time. Serendipity requires retrospective sense-making: we can only identify serendipity after it has happened, not while it is happening. Serendipity is also highly relational. Even if focusing only on external aspects, what Wellman and Berkowitz (2008: 31) refer to as social structure and process, we perceive serendipity as inter-linked and inter-dependent: process sequence matters, external context plays a role, and multiple actors, including people, things, and information, are entwined in process.
When referencing this social structure and process, or event structure, of serendipity, both theory and empirical research claim significant roles for people and information. For example, Van Andel's (1994) description of serendipity patterns, Snowden's (2005) ideas on managing for serendipity, André et al.'s (2009) discussion on designing for serendipity, and de Rond and Morley's (2010) collection of essays presenting perspectives on serendipity from a range of disciplines all refer to the roles of linking with others, both through existing and newly created links, and of knowledge discovery, transfer, use and re-use in social structure and process in serendipity. Recent research (Dantonio 2010; McCay-Peet and Toms 2010) supports these theoretical propositions concerning event structure: collaboration, including with outsiders, seems to come into play as do knowledge exchange and exposure to new ideas.
A dilemma for serendipity theory is that interactions between people and information are not unique to serendipity; these interactions are also recognised as important in the related phenomena of creativity and innovation (Fleming et al. 2007; Perry-Smith 2006; Uzzi and Spiro 2005; Zhou et al. 2009). We wish to claim the interactions between people and information as important to our theoretical understanding of serendipity, yet our existing theories lack precision and detail concerning these interactions, let alone the evidence to point to interaction patterns that could be considered unique markers of serendipity.
What, if any, normative interaction patterns do we find in serendipity? Are some interaction patterns more common than others? How are people and information related in the interaction patterns? Our work on motif detection in event structures of serendipity addresses these questions, providing precise, detailed description of normative interaction patterns. This description is important for two reasons. Firstly, the description contributes to and expands the existing serendipity knowledge base. Secondly, future research may be able to examine if the detected motif patterns are distinct markers of serendipity. If so, then such knowledge could inform theoretical models and/or simulations, which may eventually translate into practical applications in the area of systems design.
Our work on motifs was a distinct component of a larger descriptive study employing network methods to describe and measure the event structure of serendipity as recounted in narrative. The motif component aimed to detect any existence of statistically significant local interaction patterns in the event structures. Local interactions were defined as those centring on the narrators and over which the narrators may have had some direct control. If any statistically significant interaction patterns were found, then the study aimed to describe and compare these patterns, especially in terms of attributes and the narrators' positions in the patterns.
Using network methods that allowed the capture of the cumulative, retrospective and relational features of serendipity, the study analysed first person narratives that recount serendipity occurrences in research, coded the event-based aspects of these narratives, and described the coded aspects in what we term phenomenological event structures of serendipity. These event structures, which were converted into networks, describe details of event sequence and the links between actors and actions involved in the narratives' events. Because the narratives are outlined from the narrators' perspectives, the coded event structures were considered phenomenological, event structure descriptions as lived and experienced by the narrators and, crucially, deemed by them to be relevant to the occurrence of serendipity.
The raw data used in the study were extracted from the Citation Classics database, a data-set used previously in serendipity research (Campanario 1996; Hannan 2006). A Citation Classic is a one-page first-person narrative that provides the author of a highly-cited research paper the opportunity to discuss events and experiences surrounding the research not reported in the formal research report. Approximately 8% of the Citation Classics discuss some sort of luck or chance event (Campanario 1996: 10). Findings from the non-motif components of our research suggest that between 1-2% of the Citation Classics refer specifically to serendipity.
The phenomenological basis of the study demanded that the Citation Classic narrator explicitly identify an experience as serendipity: implicit references to possible serendipity, such as the mention of luck or chance, were considered insufficient for the study purposes. A keyword search of the database using the stem serendip was conducted to spot explicit references to serendipity; however, problematically, the varied semantic uses of the term meant that a few narratives included the stem while clearly not referencing a serendipity occurrence experienced by the narrator. As such, the keyword search was combined with one of the broadest serendipity classification schemes available in the literature, Campanario's two-category taxonomy (Campanario 1996: 10), to identify a sub-population of serendipity narratives. The study sample of fifty narratives was drawn randomly from this sub-population.
The study employed both narrative and network analysis methods. Narrative approaches vary widely, encompassing structural, semantic, and pragmatic aspects of narrative theory (Squire 2008: 9). Given the study's focus on event structures, we adopted an event-based approach to narrative, specifically, Labovian narrative analysis with its concept of complicating action, the actors and sequence of actions as detailed by the narrator. Reading any narrative from an event-based perspective, we sense the inherently relational nature of the story being told: actors in the story are linked by actions, creating event sequences that cumulate in an overall event structure.
Each relation between two actors in a narrative can be reduced to a semantic triplet, a linguistic-related concept most simply understood as {Subject:Predicate:Object}. A good example of the use of the idea of the semantic triplet in an information-related area is the Resource Description Framework, the metadata model used to label the conceptual linking structure of the Web we commonly refer to as the Semantic Web (Kinsella et al. 2007). The basic Resource Description Framework data model, a statement which incorporates a property to represent the relation between two resources, is a form of semantic triplet. Readers are referred to the RDF/XML syntax specification (W3C 2004), Section 2.1, for more details on this basic model.
Two points are important to the understanding of semantic triplets. The first is that despite being described in terms normally associated with syntax (e.g. subject, predicate and object), the triplet is semantic rather than syntactic. The second is that semantic triplets are always directed, a strength that allows the conveyance of meaning in structural form. Meaning is established by moving from subject through predicate to object, {Subject→Predicate→Object}.
Semantic triplets appear in various guises in the literature. Because his work focuses on the actors and actions in narrative, Franzosi (2010: 24) suggests the use of the variants {Subject→Action→Object} or {Participant→Process→Participant} (where the two participants represent different actors), while Roberts (1997: 90) uses the term, verb, instead of either predicate or action. Because our study focused on process in event-based narrative, we adopted Franzosi's {Participant→Process→Participant} label for the semantic triplet.
All network approaches allow a relational perspective on the phenomenon under study. Networks, a type of mathematical model derived from graph theory, are useful for studying relations. A network is a structure formed by a collection of elements and their interrelations (Kolaczyk 2009: 15). Networks can be represented qualitatively as network visualisations, and quantitatively as matrices or lists. The elements in a network, formally termed vertices or nodes, are often represented as dots in network visualisations; however, vertices can be visualised in a range of ways, including as symbols or thumbnail images. The smallest unit of analysis in a network is the dyad, two elements and the relation linking them. Links in network visualisations take the form of lines that can be undirected (—), one-way (→ or ←É), or bidirectional (↔Ł). Two vertices not joined by any line form a null dyad (• •). Note how the semantic triplet we discussed above represents a non-null, directed dyad (•→•), with the two participants as the vertices and the process as the line between them.
In our study, we treated the event structures of the narratives as networks. The event structures comprised the collections of semantic triplets coded from the narratives' complicating actions. The extraction of the event structures from the narratives and the conversion of these event structures into networks involved three stages. The first and second stages captured the event structures from the narratives. The techniques applied, details of which are beyond the scope of this paper, included narrative analysis to delineate the complicating actions in the narratives (Franzosi 2010; Labov 2001) and relational text analysis (also called map analysis) (Carley 1993), supported by semantic grammar (Dixon 2005), to code the semantic triplets found in the complicating actions. The coded semantic triplets were stored in Excel files. The third stage converted each set of coded semantic triplets into network format. This process was automated using Excel2Pajek (Pfeffer 2004), software designed to convert Excel files into network list files that can be read by the network analysis software, Pajek (Batagelji and Mrvar 1996). Applied sequentially, the three stages produced fifty networks as outcome.
Each of the extracted networks described the phenomenological event structure of its corresponding narrative, with the vertices representing story actors and the lines representing interactions between these actors. In keeping with network theory, the actors in our networks did not need to be capable of action in any real sense; for example, a scientist, a book and a telescope could all have been considered actors. Each of the network actors was assigned the attribute of person, object or information. The lines in our networks represented directed process interactions, which were either one-way or bidirectional.
Figure 1 shows a network visualisation of one of the fifty serendipity networks described in the study. The vertex representing the narrator is identified and the remaining network vertices are labelled by attribute.
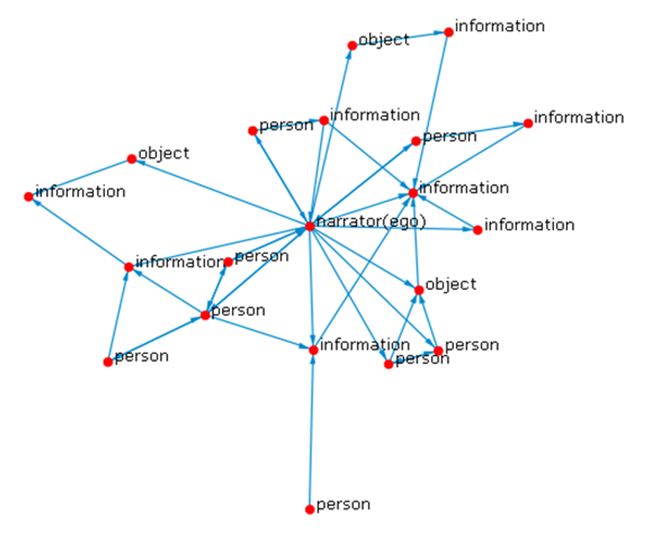
Note that in Figure 1, people, information and object vertices can be linked. It does not matter that the vertices represent actors assigned different attributes. This approach is unusual in network methods. It is common practice in network analysis to treat actors with different attributes as being in different modes and to allow only actors within different modes to interact. For example, in a network representing academics attending conferences, the academics would likely comprise one mode, let us say blue vertices, while the conferences would comprise a second, and separate, mode, red vertices, for example. In this two-mode network, the academics could only link to each other through conferences, blue vertices to red vertices: no direct links between academics, blue vertices to blue vertices, could ever exist.
Despite this common stance on mode, network methods ultimately place the decision to use a single or multi-mode approach with the individual analyst and recognise that mode choice is guided by the research aims (Borgatti and Everett 1997: 244). We adopted a one-mode approach in our study. An inherent aspect of such an approach is that no restrictions are placed on how vertices in a network can link. Thus, the one-mode approach allowed us to avoid forcing assumptions on our data about the importance or role of attribute relations in event structure.
Much of the study analysis and reporting focused on relations involving the special case of the narrator, or ego vertex, in each of the serendipity networks. Network analysis that focuses on ego is termed egocentric and is concerned with exploring the ego network, a network comprising ego and all of his alters, other network actors linked directly to ego. Ego networks are usually described at a distance of one link away from ego and include, not only ego's links to alters, but also alters' links to alters. In our study, the ego networks are reduced versions of the complete serendipity networks. In the serendipity stories, the narrators describe events in which they are directly involved (links at a distance of one) and events in which they are only indirectly involved (links at a distance of more than one). Both types of events combine to result in serendipity; however, we were interested most in the events in which the narrator could take direct action and/or have direct effect as these represent the events over which ego could have some direct control.
Figure 2 illustrates the ego network extracted from the serendipity network presented in Figure 1.
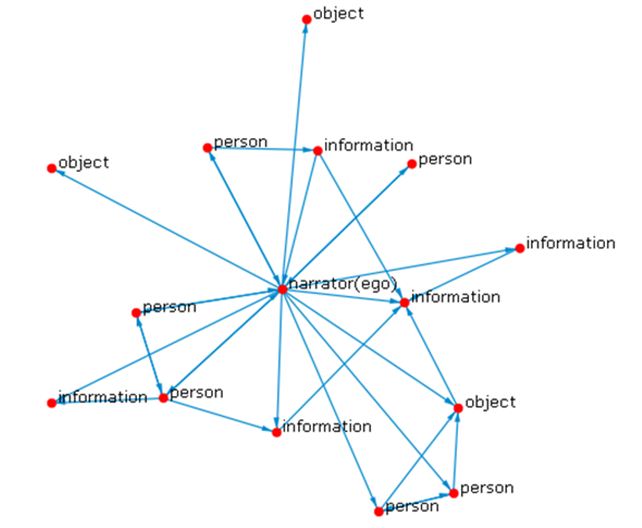
Notice that the extracted ego network illustrated in Figure 2 is smaller than the complete serendipity network shown in Figure 1. As the network statistics presented in Table 1 demonstrate, the ego network has lower vertex and line counts.
| |
Vertex Count | Line Count |
|---|---|---|
| Complete network | 20 | 41 |
| Extracted ego network | 15 | 31 |
Before moving to our discussion of motifs, we need to establish one more concept essential to the interpretation of the serendipity networks, i.e., sequence, or the representation of time in the event structure. In the discussion above, we refer to the semantic triplet as a directed dyad (•→•) yet also mention that lines in our study networks were either one-way or bidirectional. Given that the line in the semantic triplet as directed dyad is one-way, how is it possible that the serendipity networks in our study contained bidirectional lines?
The reason is that bidirectional dyads actually represented two semantic triplets combined, a mutual interaction between two actors, most often people, in the serendipity network. For example, the first semantic triplet, {parent hugs child}, and the second semantic triplet, {child hugs parent}, combine in the bidirectional dyad representing mutual interaction, (parent ↔Ł child). Even when an interaction is mutual, it rarely, if ever, is initiated in both directions at exactly the same moment in time. In the hugging example above, either the parent or the child likely made the first move, even if the hug appears to an observer to be initiated by both parties at exactly the same time. It is a feature of narrative that narrators are usually quite precise about sequence, telling us clearly, for example, who started the hug. While it is tempting to associate sequence with cause and effect, for example, that by starting the hug, the parent caused the child to hug back, sequence is a separate concept. The child could have hugged back because it felt sad, not because the parent hugged it first.
Although information about sequence, or time event data, was captured and stored in the course of our research, visualisation of this data would have been extremely time consuming and complex. As such, the visualisations of the serendipity networks described only cumulative event structures. Because the time event data is missing from the networks, we were careful to avoid network analyses that rely on the idea of sequence flowing through the network. As is the case in all network studies, issues of cause and effect were also not addressable using the network visualisations alone. When exploring any of the network visualisations from the study, including motifs, we must remember that what we are seeing is a structure built from overlapping, cumulative sequence, not flow, Łand certainly not cause and effect, Łand draw our conclusions accordingly.
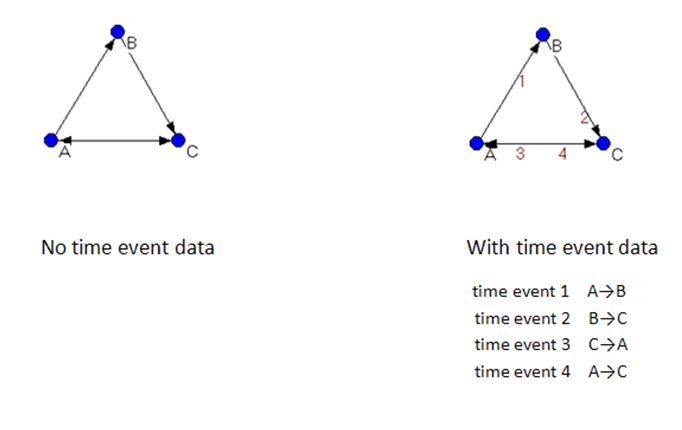
Figure 3 illustrates the limitations caused by the lack of time event data in a cumulative network visualisation, the dangers of cause and effect approaches, and the need for care in interpretation. The network on the left contains no time event data, while the network on the right does. While in the network without time event data, it appears that A interacts with C on the same basis as with B, it is clear from inspection of the network containing time event data, that A only interacts with C after C has initiated an interaction with A. From the network visualisation alone, we have neither information to tell us if A would have interacted with C had C not initiated an interaction nor information to tell us if B's interaction with C caused C to initiate an interaction with A.
Having established the idea of a network extracted from a serendipity narrative, the basics of an egocentric approach to such a network, and the limitations and interpretation dangers involved, let us return now to the concept of the network motif in light of our discussion. As introduced earlier in this paper, the idea behind motifs is that they are sub-structures of a larger structure. But a motif is not just any sub-structure; it is traditionally interpreted as a key and recurring sub-structure, a defining building block in the larger structure.
Because, as we have seen, networks are relational objects, care must be taken when using mathematical or statistical methods to compare networks of different sizes (those comprising different numbers of vertices). Even when the number of vertices in two networks is the same, the number of lines and the way the vertices are linked may differ, making some direct quantitative comparisons impossible. One approach to dealing with the problem of comparing networks of different sizes is to employ statistical comparison techniques that depend on the simulation of random network models generated algorithmically using computer software. Put simply, network statistical comparison techniques generate an ensemble of random networks of the same size as a given real network, for example, a serendipity network. Then, because the networks involved are the same size, the generated ensemble and the real network can be directly compared for statistical purposes.
A random network model is a mathematical model that includes both fixed and randomly-determined parameters. A single random network on its own is not much use for statistical comparison purposes; when we refer to the use of random network models in statistical comparison techniques, we are actually referring to the use of an ensemble of random networks. Newman (2010: 566) defines an ensemble as, 'a set of possible networks plus a probability distribution over them'. The Erdös-Rényi model is one example of a random network model. In this model, the number of network vertices is fixed by the modeller, but the number of network lines and the way they are distributed between the vertices is determined by probability. Readers interested in more detail about the types and properties of random network models may wish to consult Part Four, Network models, of Newman (2010).
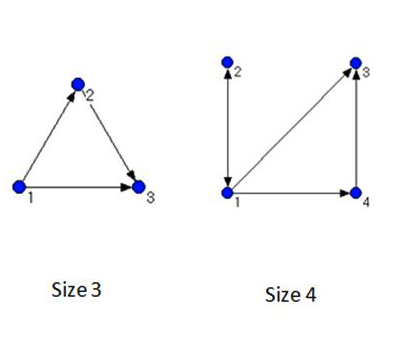
Network motif detection, a form of statistical comparison reliant on the use of random network models, traditionally involves looking for motifs of size 3 or 4, containing three or four vertices respectively, and requires the use of computer software. Figure 4 presents examples of size 3 and size 4 network motifs.
In our study, we analysed the size 3 motifs involving ego contained within the serendipity networks. This choice was driven in part by theoretical concerns. Size 3 motifs represent the simplest possible interaction pattern possible in a network above the basic unit of analysis, the dyad. In a size 3 motif, ego must always be involved in a minimum of one direct interaction and a maximum of two, meaning that ego has at least a 50% chance of being involved in a direct interaction, the type of interaction of that was of interest to our study. In size 4 or higher motifs, ego's chance of being involved in indirect interactions increases because of the potential for more dyads occurring that do not involve ego. Figure 5 illustrates this point.
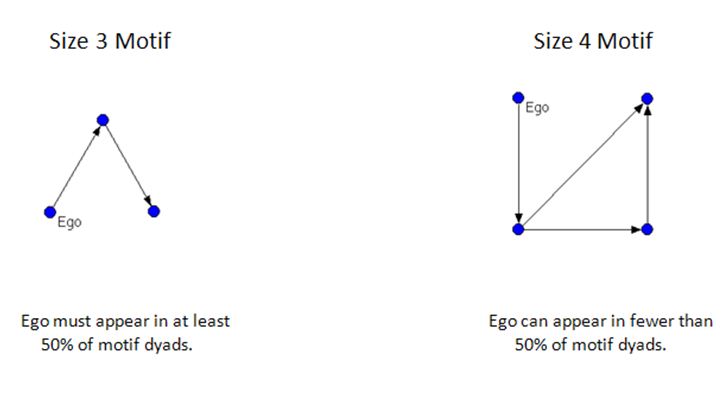
The choice of motif focus was also driven by methodological concerns. Like the larger serendipity networks in our study, the extracted network motifs, too, were visualised; therefore, the implication of these networks as representations of cumulative structure demanding the need to avoid the idea of sequence flowing through the network applied equally to the motifs. Limiting detection to size 3 motifs permitted a view on interaction from ego's perspective that did not need to be based on flow or sequence.
The number of possible size 3 motifs in any network is mathematically limited to sixteen. Figure 6 illustrates these sixteen possibilities.
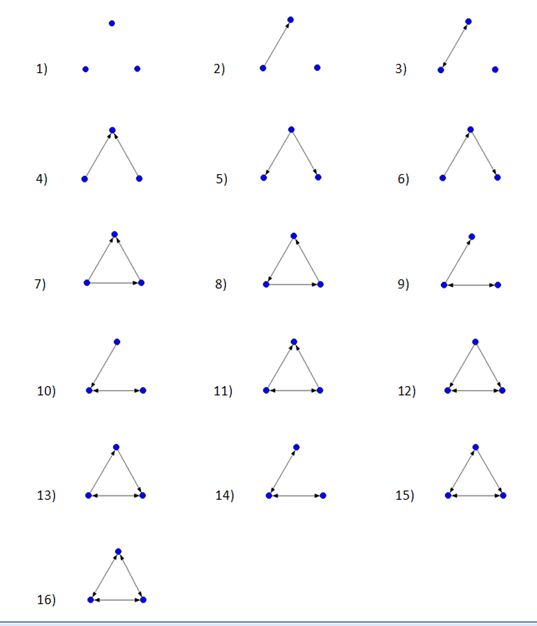
Note that motifs 1 to 3 contain null dyads. Because all of the serendipity networks were fully connected, meaning that every vertex in each network was connected to at least one other vertex in that network, the first three motifs in Figure 5 were never found in the serendipity networks. As such, only thirteen possible size 3 motifs were relevant to the study.
Regarding motifs, the study's analysis objectives were threefold:
For the analysis, we employed the Fast Network Motif Detection (FANMOD) software. For more details on this software and the specific algorithm it uses, see (Wernicke and Rasche 2006) and (Wernicke 2006). Each of the fifty serendipity networks was subjected to a separate statistical comparison test against 1,000 algorithmically generated random network models. In the random model set-up, the option to keep the number of bidirectional lines locally constant was selected. The number of exchanges per line and the number of exchange attempts were both set to three. The output parameters were set to judge motifs for which the Z score was >2 and the p-value was <0.05 as statistically significant. We did not require a motif to occur a minimum number of times or above a certain frequency. Once the software had detected the motifs within the individual serendipity networks, the results were examined manually to count the number of networks containing each motif and to determine details of line direction and attribute spread for each motif.
Twelve out of the thirteen possible size 3 motifs were found to be statistically significant in the serendipity networks: nine involved ego and three never did. Approximately two thirds (33/50 or 66%) of the serendipity networks contained motifs; of these, thirty involved motifs containing ego. The three networks containing motifs not involving ego may be different in some way; however, closer examination of these outliers did not shed any light on the reason for this difference. It was not possible to check for motifs in two of the fifty networks due to faulty output returned from the computer analysis. The input data files of these two networks were examined for problems; however, as none were found, the faulty outputs were assumed to result from a software bug.
Four motifs involving ego were identified as dominant across the remaining forty eight networks. Figure 7 illustrates these motifs.
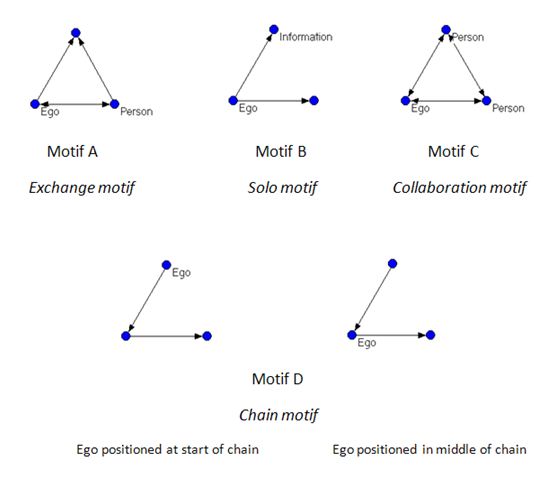
Motif A, nicknamed the exchange motif, occurred in twenty one networks. This motif involves ego linked by a bidirectional line to another person and both ego and that other person linking to the third vertex in the motif, with this third vertex most often representing information. Motif B, dubbed the solo motif, was found in thirteen networks. Ego is the sole person in this motif and links by one-way lines to the two other vertices, at least one of which is always information. The second vertex is usually information, but occasionally an object or a person. Motif C, labelled the collaboration motif, appeared in twelve networks and involves ego and two alters, both people, all linked to each other by bidirectional lines.
Motif D, termed the chain motif because of its pattern forming a chain of one-way links, occurred in fourteen networks and exhibited more complex behaviour in comparison to the other motifs detected. In all fourteen examples, the chain motif appeared with ego positioned at the start of the chain, with the other vertices in the chain almost exclusively information and objects; however, in three of the fourteen networks, ego also appeared in the mid-position in the chain. In two of these mid-chain cases, the vertex occupying the starting position in the chain was a person whose only link in the network was to ego.
Our motif findings contribute description of interaction patterns in serendipity and raise several questions. The findings are evidence that interaction patterns do appear and repeat with statistically significant frequency in event structures of serendipity. Our work on motifs provides precise, detailed description of the attribute and link patterning in these interactions. Four interaction patterns were noticeably dominant, with one, the exchange motif, appearing considerably more often than the others. The serendipity networks were of many sizes and represented seemingly highly heterogeneous narrative accounts of serendipity; however, the narrators, despite the heterogeneity of their serendipity accounts, appeared consistently in the same positions in the dominant detected motifs.
The spread of attributes in the motifs differed subtly from the overall attribute spread in the ego networks. Findings from the larger research project indicated that, on average and excluding ego, the ego networks extracted from the serendipity networks comprised 48% information, 37% people, and 14% objects. Information and people also dominated the motifs; however, bearing in mind that one dominant motif, the collaboration motif, included only people, the attribute spread in the motifs may indicate that people are more highly represented in the motifs than in the ego networks.
The attribute patterning found in the dominant motifs was also notable. Given the nature of the serendipity event structures, structures in which people were more likely than information or objects to have bidirectional links, it was not surprising that all of the bidirectional links in the motifs were between people; however, links between people were not exclusively bidirectional. The exchange, solo, and chain motifs all presented occasional one-way links from person to person.
More generally, the attribute consistency of the one-way motif dyads was unexpected. For example, the finding that, out of the two possible one-way links in the solo motif, one link always connected ego to information was a surprise. Although, at 14%, objects comprised the smallest attribute division in the ego networks, we might reasonably have expected at least a few occurrences of the solo motif where ego linked to two objects, two people, or to an object and a person.
The detection and description of statistically significant interaction patterns raises questions for serendipity theory: why are some interaction patterns more dominant than others? if the same dominant patterns appear, regardless of the heterogeneity of contexts and events, then what roles do context and events play? why do the dominant patterns show such consistency in attribute patterning? why does ego consistently occupy the same position in the dominant motifs? could these dominant patterns, or a combination of them, be unique markers for serendipity?
In addition to the questions they raise for future research, the motif findings have immediate implications for our theoretical understanding of serendipity. The findings do seem to support the references to the importance of people and information we claim in theories of serendipity; however, the findings also suggest that the roles of people in serendipity may be more subtle than our theories commonly assume. For example, our theories sometimes focus on collaboration as a significant feature of serendipity. Indeed, existing applications aimed at enabling serendipity actively attempt to encourage this feature (Eagle 2004; Eagle and Pentland 2004). The exchange motif, with its interaction between ego and another person, was by far the most dominant of the motifs detected, seeming to support this theoretical leaning towards associating collaboration with serendipity. Nonetheless, the appearance of individuals other than ego was rare in two of the other four dominant motifs detected, the solo motif and the chain motif. This finding, in combination with the fact that in some of the serendipity networks studied, ego was the only person in the network, serve to remind us that social interaction is not a necessary condition of serendipity.
The prospect of normative interaction patterns in serendipity is also given weight by our findings. While without further research on different data, we can only argue that our findings indicate that some interaction patterns may be normative in our study population, this finding is a theoretical step forward, contributing empirically-based detail to the currently imprecise notion of normative behaviour in serendipity. The narratives in our study recount serendipity occurring in the sciences and social sciences. The breadth of these accounts is very narrow in some ways: most are in science rather than the social sciences, many occur in lab-based contexts, and medicine is a dominant subject area. Yet the narrative data are highly heterogeneous, lending weight to the possibility that any commonalities found across the sample, such as motifs, may indeed be indicative of norms. If norms exist, then they may not be limited to our study population.
The motif findings must be seen in light of the standard limitations that affect all findings resulting from motif detection. First and foremost, the concept of motifs as important, defining building blocks in a network remains theoretical. As any researcher knows, it is all too easy to see patterns everywhere. While we may extract patterns from a larger structure, it does not follow that these patterns must inform the structure: logically, conceptually and empirically, the order {structure first, patterns second} need not equate to {patterns first, structure second}.
Secondly, there are limits to the idea of statistical significance in the context of motifs. Motif detection focuses on frequency, which must not be confused with importance. Something may occur a lot, but another thing that occurs only once may be the crucial element.
Thirdly, the detected motifs provide only selected information about event structure, not the full picture. In turn, event structure is a simplified model that provides information on only one aspect of serendipity's duality. In our study, the motifs, like the networks in which they occurred, represented cumulative structure. Although it is tempting to imagine the two individuals in the exchange motif interacting in a single discussion over morning coffee, the true picture may be much more complex; for example, the interaction may have occurred over the space of years rather than in one setting.
Finally, while we can claim that motifs exist in our study networks, our research represents an initial, exploratory foray into the area of motif detection in serendipity. The research area needs considerable development before any claims are made that certain motifs, either alone or in combination, are distinct markers of serendipity. For example, the motifs we detected may be common to other phenomena such as creativity or innovation, or they may even be a function of narrative itself, regardless of the narrative topic.
Narratives contained in the Citation Classics database offered an opportunity to study the phenomenological event structure of serendipity and to investigate the possibility of motifs, frequently repeating patterns and possible building blocks of larger structure, occurring in serendipity. After describing the narratives as networks, motif detection methods were employed to identify statistically significant interaction patterns in the event structures of serendipity.
Four dominant motifs emerged from the analysis as occurring frequently in the serendipity networks: the exchange motif, the collaboration motif, the solo motif, and the chain motif. The motifs were notable both for their focus on the attributes of people and information and the uniformity of their interaction patterns with regards to these two attributes. The motifs were detected in many different sizes of networks that represented seemingly highly heterogeneous narrative accounts of serendipity; yet, time and time again, the same dominant motifs were detected and the narrators occupied the same positions in these motifs.
The motif findings have theoretical implications, supporting ideas relating to the importance of people and information in serendipity while acting as a reminder that social interaction is not a necessary condition of serendipity. The findings also provide initial evidence for normative interaction patterns in serendipity, suggesting that this line of enquiry may be ripe for theoretical development. When considering the motif findings, it is important to remember that the theoretical basis for the concept of motifs as important to structure, limits to the idea of statistical significance in the context of serendipity, and the simplified nature of the network models in combination with the narrative data used in the study all necessarily guide the interpretation of the research findings.
The research presented in this paper provides empirical evidence for the existence of statistically significant interaction patterns in phenomenological event structures of serendipity. Our findings should be viewed as an initial, exploratory contribution; while motif detection opens some interesting, new theoretical and empirical doors on serendipity, this line of research is very much in its infancy. We hope that, in future, others will continue to explore the potential of motifs in the context of serendipity research.
Abigail McBirnie undertook the data collection, carried out the analysis, and drafted the paper. Christine Urquhart advised on aspects of the research and reviewed the draft.
In addition to the software used during the research and referenced in the body of this paper, we also used software to create the figures illustrated in the paper. Batagelj and Mrvar's Pajek (http://pajek.imfm.si/doku.php?id=download) and Carley's ORA (http://www.casos.cs.cmu.edu/projects/ora/software.html) both network analysis programs, facilitated the creation of the illustrated networks and motifs. We employed TechSmith's Jing (http://www.techsmith.com/jing) to capture the screenshots of the network and motif figures presented in the paper.
Abigail McBirnie is a PhD research student at Aberystwyth University. A qualified librarian, Abigail initially trained as a musician. Most recently, she held the position of Assistant Professor of Library Science and Music at Oklahoma City University. She can be contacted at amcbirnie@googlemail.com.
Christine Urquhart is a Senior Lecturer in the Department of Information Studies, University of Aberystwyth. Her main research interests are in information behaviour and information systems research and health information management. She is a co-author of several systematic reviews for the Cochrane Collaboration and is also interested in meta-synthesis of qualitative research. She can be contacted at cju@aber.ac.uk.
| Find other papers on this subject | ||
|
© the authors, 2011.
Last updated: 27 August, 2011 |
|
|
|