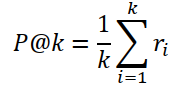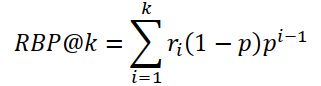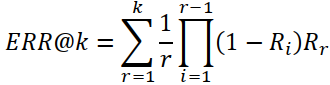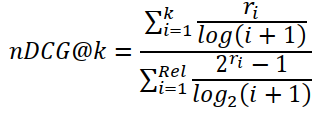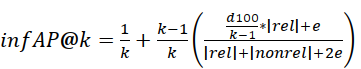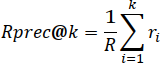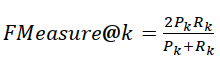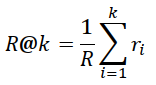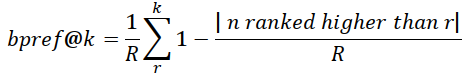Correlation and prediction of high-cost information retrieval evaluation metrics using deep learning
Sinyinda Muwanei, Sri Devi Ravana, Wai Lam Hoo, Douglas Kunda, Prabha Rajagopal, and Prabhpreet Singh Sodhi
Introduction. To reduce cost of the evaluation of information retrieval systems, this study proposes a method that employs deep learning to predict the precision evaluation metric. It also aims to show why some of existing evaluation metrics correlate with each other while considering the varying distributions of relevance assessments. It aims to ensure reproducibility of all the presented experiments.
Method. Using data from several test collections of the Text REetrieval Conference (TREC) we show why some evaluation metrics correlate with each other, through mathematical intuitions. In addition, regression models were used to investigate how the predictions of the evaluation metrics are affected by queries or topics with variations of relevance assessments. Lastly, the proposed prediction method employs deep learning.
Analysis. We use coefficient of determination, Kendall's tau, Spearman and Pearson correlations.
Results. This study showed that the proposed method performed better predictions than other recently proposed methods in retrieval research. It also showed why the correlation exists between precision and rank biased precision metrics, and why recall and average precision metrics have reduced correlation when the cut-off depth increases.
Conclusions. The proposed method and the justifications for the correlations between some pairs of retrieval metrics will be valuable to researchers for the predictions of the evaluation metrics of information retrieval systems.
DOI: https://doi.org/10.47989/irpaper920
Introduction
Information retrieval is finding documents that satisfy the user's information need from large document collection (Manning et al., 2008). Users with the information need formulate a query and submit it to the information retrieval system that accepts the query as input and produces a ranked list of documents. Ideally, the ranked list should only contain relevant documents ordered according to their degree of relevance. In reality, however, the situation is different. A query submitted to two information retrieval systems will not produce identical ranked lists. This is because information retrieval systems differ in how they produce ranked lists. This means that one information retrieval system may return a ranked list with more relevant documents than the other. To find out which information retrieval system is better, there is need to evaluate them. In the field of information retrieval, the popular approach to evaluate retrieval systems uses test collections. A test collection comprises a corpus of documents, predefined topics (i.e., queries), and a query relevance file containing a set of relevance judgments. For instance, in binary relevance settings, if a document is relevant to a topic, then there would be an entry of one in the query relevance file for that topic, otherwise the entry would be zero. These relevance judgments are manually generated by expert assessors. To evaluate a particular retrieval system, the queries in the test collection are used by the retrieval system being evaluated to retrieve a set of documents. These retrieved documents per query are compared against the relevance judgments entries in the query relevance file in the test collection and the effectiveness of the evaluated retrieval system is determined depending on how many relevant documents were actually retrieved by using appropriate evaluation metrics.
Though this evaluation approach has been used for decades, it still has several drawbacks. The most crucial drawback is the cost of generating relevance judgments (Moghadasi et al., 2013) and this is largely due to the manual generation of the relevance judgments. The aim of this study is to provide a proposal that contributes to the reduction in the use of relevance judgments and consequently reduces the cost of these judgments. In addition, this study aims to show why some correlations exist among evaluation metrics. Many correlations between evaluation metrics have been identified in information retrieval research, but less attention has been devoted to show why those correlations actually exist. In recent research (Gupta et al., 2019), a proposal was made to reduce the cost of generating the relevance judgments through the prediction of the evaluation metrics at the high cut-off depths of documents while using the evaluation metrics computed at the low cut-off depths. In the same research, evaluation metrics computed at the cut-off thresholds of at least 100 documents were referred to as the high-cost evaluation metrics. In our study, we adopt this naming of evaluation metrics. Much as this proposal of predicting high-cost metrics is worthwhile, Gupta et al. reported that only the prediction of the rank biased precision high-cost evaluation metric was accurate while using low-cost evaluation metrics computed at the cut-off thresholds of up to thirty documents. At the same cut-off threshold (i.e., thirty documents) for the low-cost evaluation metrics, the high-cost precision metric was worst predicted. Therefore, this study focuses on the prediction of the high-cost precision metric using other metrics computed up to the maximum cut-off depth of thirty documents. Further, researchers in information retrieval have reported several correlations between evaluation metrics. However, justifications for most of these correlations are lacking. Hence, this study also fills this gap by providing justifications of some of these correlations between the evaluation metrics. Furthermore, this study also investigates the effect of the distributions of relevance assessments on the correlations of evaluation metrics.
This study has four objectives:
- To show why the correlation reported in the previous studies between precision and rank biased precision metrics exists.
- To show why the increase in the cut-off depth of documents leads to a reduced correlation between recall and average precision.
- To show the effect of the distributions of relevance assessments on the correlations of the rank biased precision and the precision evaluation metrics as well as the correlations of the recall and average precision evaluation metrics.
- To present a method that employs the stacked generalization deep learning ensemble to predict the high-cost precision metric in information retrieval evaluation.
Reproducibility has become a matter of concern in information retrieval research. Therefore, to enhance reproducibility, a dedicated section has been included highlighting reproducibility issues and how they have been addressed in the study.
The remaining part of this paper proceeds as follows. Section two presents related work. Section three presents reproducibility in information retrieval evaluation; Section four presents the methodology of the study. Section five presents the results and discussion, and section six presents the conclusion and future work.
Related work
This section describes prior work on correlations between information retrieval evaluation metrics and low-cost information retrieval evaluation methods. Baccini et al. (2012) investigated the correlations between 130 measures using relevance judgments and runs from Text REetrieval Conference (TREC) (2-8). The authors used principal component analysis and hierarchical clustering to group the measures into seven homogeneous clusters. However, this study only considered binary relevance and lacked justifications for the observed correlations among measures. Tague-Sutcliffe and Blustein (1995), analysed seven measures on TREC-3 and their findings indicated average precision and R-precision are highly correlated. Aslam, Yilmaz and Pavlu (2005) presented a geometric interpretation of R-precision and its correlation with average precision. Sakai (2007), Thom and Scholer (2007) and Webber et al. (2008) also investigated the correlations of evaluation measures. More recently, the study by Gupta et al. (2019) investigated the correlations of twenty-three evaluation metrics using eight Web and Robust TREC tracks. All these investigations into correlations were based on empirical observations of data. Our study complements this work by providing mathematical intuitions for correlations between precision and rank biased precision as well as recall and average precision. Further, our study presents a method for predicting high-cost precision metric as a solution to reduce costs in information retrieval evaluation. Therefore, this literature review focuses on previous studies that investigated methods of reducing costs in information retrieval evaluation.
Constructing test collections is costly, particularly in the human effort required to generate relevance judgments. Prior research has investigated a variety of methods to reduce costs in the test collection model of system-based information retrieval evaluation. These methods encompass inference of relevance judgments, finding the documents to be judged per topic, topic selection, evaluation with no human judgments, development of measures that are robust to incomplete relevance judgments, inference of evaluation metrics and, more recently, crowdsourcing.
Several proposed methods exist for inferring relevance judgments. Aslam and Yilmaz (2007) proposed a method that infers complete judgments given a few judged documents. The authors showed that the proposed method produced inferred relevance judgments that evaluate systems in the same way as actual relevance judgments; the relevance of documents in the inferred relevance judgments produced by the proposed method were very similar to the actual relevance judgments from TREC. Rajagopal et al. (2014) proposed a method called the cut off percentage which automatically generates relevance judgments. The authors reported that the greater the number of occurrences of a document per topic in various TREC runs, the higher the possibility of the relevance of the document. Besides, the proposed method uses a pool depth of 100 and a cut-off percentage of greater than 35 per cent. The authors also showed that their method produced higher Kendall's tau correlations when compared with the method proposed by Soboroff et al. (2001) on the same TREC tracks. Other studies (Büttcher et al., 2007; Makary et al., 2017), also investigated the construction of relevance judgments without human assessors.
Some researchers have proposed methods for finding the best documents to be judged per topic in the process of constructing relevance judgments. Zobel (1998) proposed a method for pooling that increases the number of relevant documents found for judgment efforts. The author reported that though the method uses simple regression that is approximate, it returned more relevant documents and this should increase the reliability of measured results in large scale information retrieval experiments. In other research, Carterette and Allan (2005) proposed a method that constructs relevance judgments through intelligently selecting documents to be judged and decides when to stop document selection. The authors showed that the proposed method achieved high Kendall's tau rank correlation with fewer relevance judgments when evaluating TREC ad hoc submissions. However, the authors reported the lack of formal proofs for the proposed method and the need to investigate better weighting schemes and stopping conditions. Other studies have also investigated the document selection for judgment (Cormack et al., 1998; Carterette et al., 2006; Losada et al., 2017; Moffat et al., 2007).
A growing body of literature has investigated low-cost information retrieval evaluation through topic selection. Carterette et al. (2008) proposed the usage of fewer relevance judgments in information retrieval evaluation. The authors presented the results of the Million track of TREC 2007 and investigated the trade-offs between the number of queries and the number of judgments. Their findings showed the cost-effectiveness of the evaluation over more queries with few judgments was equally as reliable as fewer queries with more judgments. They also reported that total assessor effort could be reduced by 95% without a notable increase in evaluation errors. Hosseini et al. (2012) proposed an uncertainty aware query selection model for evaluation of information retrieval systems commonly referred to as adaptive. The authors showed that the queries chosen by this model produced reliable performance ranking of systems. They also showed that the ranking produced by their model correlates better with the actual system rankings than the rankings produced by queries selected using the considered baseline methods. However, the authors only considered the uncertainty of the system's performance due to partial relevance judgments and errors in the relevance judgments that the human assessors made. Therefore, other sources of uncertainty could be further explored. Other studies to investigate the topic selection method include Berto et al. (2013), Guiver et al. (2009), Hosseini et al. (2011), Kutlu et al. (2018), Rahman et al. (2019), Roitero et al. (2019), and Sanderson and Zobel (2005). ; Interested readers are referred to a comprehensive review of low-cost information retrieval evaluation methods conducted by Moghadasi et al. (2013).
Various studies investigated the estimation of the evaluation metrics in information retrieval evaluation. Aslam et al. (2005) proposed a method that estimates evaluation measures using a corresponding retrieved ranked list. The authors concluded that user-oriented measures such as precision can be inferred from system-oriented measures such as average precision and R-precision. Ravana et al. (2009) proposed an exponential smoothing estimation method which combines the result of a previous information retrieval evaluation experiment with a new observation to estimate a reliable system score. In another study, Yilmaz and Aslam (2008) proposed the inferred average precision measure that accurately estimates average precision when judgments are not complete. More recently, Gupta et al. (2019) proposed the prediction and ranking methods of evaluation metrics in information retrieval. The authors analysed the correlation between twenty-three information retrieval metrics and used a simple linear regression model to show that an accurate prediction of an evaluation metric can be achieved using only two or three other metrics. Additionally, the authors proposed a method that uses a linear regression model to predict the high-cost evaluation metrics using lower-cost ones. Furthermore, the authors introduced a novel ranking method that is based on covariance for ranking top metrics which enables the selection of best metrics from clusters with lower time and space complexity than required by prior work. However, using other metrics as features computed at the cut-off depth of thirty, this method made an accurate prediction for the high-cost rank biased precision metric only and the study lacked justifications for the correlations between the reported twenty-three information retrieval evaluation metrics. Therefore, our study complements the research by Gupta et al. (2019) in various ways. Firstly, we provide justifications of correlations between some information retrieval evaluation metrics, investigate how the predictions of the high-cost evaluation metrics are affected by the difficulty of topics (this difficulty of topics is largely due to variations of relevance assessments in test collections), and propose an effective method for predicting the high-cost precision evaluation metric using deep learning.
Reproducibility in information retrieval evaluation
Reproducibility refers to the ability of the research community to repeat prior work of other researchers with intent to validate the reported scientific results. The results produced after the reproducibility effort can be used to compare with other new approaches (and the reproduced work is further tested on other platforms and using different datasets to check the robustness of the methods in prior work (Fuhr, 2018). In information retrieval evaluation, reproducibility has become a matter of concern, and this has led to reproducibility tracks in information retrieval conferences such as the European Conference of Information Retrieval. In information retrieval evaluation, there are several barriers to reproducibility and the first barrier concerns data accessibility. This barrier mostly affects studies where the data that has been used is proprietary and inaccessible to the research community (Ferro et al., 2016). Also, for retrieval evaluation experiments where the development of private test collections is a requirement, the processes involved in the build of the test collections are usually not well documented. The second barrier concerns the lack of availability of the implementations of the experiments in the prior work and this might lead to the failure of the reproducibility efforts (Papariello et al., 2020). Also, the proposed methods in the prior work may not have been adequately described. The last barrier is the size of the test collections which are large and require significant storage and computation resources (Ferro et al., 2016).
To address the barrier of data accessibility, our study employs test collections from the TREC and these are the mostly used test collections for the information retrieval evaluation research. Secondly, our study has provided the clear procedures of how the evaluation metrics were computed at the various evaluation depths of documents. To address the barrier of the lack of implementations of experiments, code has been provided for the experiments reported in this study to ensure easy reproducibility of the results (Muwanei, 2021). Concerning the barrier of inadequate descriptions of proposed methods, this study provides detailed experimental procedures for all the experiments conducted. Lastly, regarding the size of the test collections, this barrier does not concern this study as only runs and relevance judgments are of interest and these usually have the size range of several hundred megabytes of data.
Research method
This section covers the methodology followed when investigating the correlations of the evaluation metrics and the methodology followed when investigating the predictions of high-cost precision evaluation metrics.
Research method for investigating correlations of information retrieval evaluation metrics
This study investigated the correlations between the precision and rank biased precision as well as recall and average precision. Gupta et al. (2019) established the existence of the correlation between precision and rank biased precision metrics, though the observed correlations were not justified. Also, justification has so far not been provided for the reduced correlations between recall and average precision when the cut-off depth increases. Furthermore, the question concerning distributions of the relevance assessments and their effects on the correlations of these evaluation metrics has not yet been answered. Therefore, firstly, the justification is provided using mathematical intuitions for the existence of the correlation between the precision and rank biased precision metrics. In addition, a mathematical intuition is also provided which shows why recall and average precision have reduced correlation when the cut-off depth increases. In both justifications of the correlations of the pairs of evaluation metrics, the mathematical intuitions also comprise detailed investigations of the behaviour of functions representing these metrics. To validate the mathematical intuitions, the Pearson correlations are computed for the pairs of metrics using TREC 2000 data. These mathematical intuitions and computed correlations are explained in the results and discussion section below.
Secondly, the effects of the distributions of the relevance assessments on the correlations of these pairs of evaluation metrics are investigated. To achieve this, an experimental procedure is employed that uses the clustering approach of the topic scores of evaluation metrics and this procedure is outlined in the following six steps:
- Compute the topic scores for the rank biased precision, precision, recall and average precision evaluation metrics. The result of this step is a set of topic scores of the highlighted evaluation metrics computed at the cut-off depths ranging between ten and 100 documents.
- For each run in the test collection of interest, compute at various evaluation depths, the proportion of unjudged documents returned for every represented topic in the test collection. The result of this step are sets that show proportions of relevance assessments for each run per topic in the test collection.
- In this step, append the results of step 1 to the results of step 2. The result of this step is a set containing the topic scores of the rank biased precision, precision, recall and average precision metrics as well as proportions of relevance assessments for each run per topic.
- In this step, create two samples of topic scores of evaluation metrics. These samples are based on the proportions of relevance assessments for each run per topic in the test collection. The first sample has between 0 and 50 per cent of the returned documents in the run per topic not present in the query relevance file, while the other sample has between 50 and 100 per cent of the returned documents in the run per topic not present in the query relevance file. Therefore, the outputs of this step are samples of topic scores with varying represented proportions of relevance assessments.
- Using the samples of topic scores of evaluation metrics generated from the previous step, compute Pearson correlations for each pair of the evaluation metrics under investigation.
- Compare the results from the previous step and identify any trends as regards the correlations of the pairs of evaluation metrics in the two samples.
Research method for the predictions of information retrieval evaluation metrics
For the prediction task, runs and relevance judgments of selected TREC tracks were the collected data, which was later prepared and used to generate training and test data sets. The development of the proposed method that employs the stacked generalization deep learning ensemble to predict the high-cost precision metric using other metrics computed at the lower cut-off depths proceeded in phases. These phases are: node analysis, layer analysis, ensemble analysis, creation of the method with stacked ensembles fitted on the training set, computation of the coefficient of determination, Kendall's tau and Spearman correlations on test sets and performance analysis. In addition, the keras framework was used for the implementation due to its ease of use hence promoting reproducibility of experiments. The following subsections describe the details of the methodology.
Data collection
The data collected for this research is in the form of runs and relevance judgments from several Web and Robust tracks of TREC. TREC is a series of workshops organised by the National Institute of Standards and Technology focusing on research in information retrieval. Annually, TREC focuses on specific research areas or tracks. In this research, selected Web and Robust track relevance judgments and runs were used from TREC tracks listed in Table 1.
| Test collection | Year | Purpose | Document collection | Number of systems | Topics |
|---|---|---|---|---|---|
| Web Track 2000 (Voorhees and Harman, 2000) | 2000 | To create a test collection that mimics the environment of the World Wide Web | WT10g | 105 | 451-500 |
| Web Track 2001 (Voorhees and Harman, 2001) | 2001 | To investigate the retrieval behaviour when the collection being searched is a large hyperlinked structure like World Wide Web. | WT10g | 97 | 501-550 |
| Robust Track 2004 (Voorhees, 2004) | 2004 | To improve the consistency of ad hoc retrieval task by focusing on poorly performing topics | Trec Discs 4&5 | 110 | 301-450 601-700 |
| Web Track 2012 (Clarke, Craswell and Voorhees, 2012) | 2012 | To examine and assess Web retrieval on large collections of Web data | ClueWeb’09 | 48 | 151-200 |
| Web Track 2013 (Collins-Thompson et al., 2013) | 2013 | To examine and assess Web retrieval on large collections of Web data | ClueWeb’12 | 59 | 201-250 |
Dataset preparation
The information retrieval evaluation metrics computed at various cut-off depths were used features. An information retrieval evaluation metric measures the capability of a retrieval system to return relevant documents. Similar to Gupta et al. (2019), the metrics used in this study are: precision, inferred average precision (Yilmaz and Aslam, 2008), expected reciprocal rank (Chapelle et al., 2009), binary preference (Buckley and Voorhees, 2004), non-cumulative discounted gain (Järvelin and Kekäläinen, 2002) and rank biased precision (Moffat and Zobel, 2008). The choice of metrics was driven by their robustness to incomplete judgments in the test collections and previous studies that investigated their respective correlations. This study also included recall, F-measure and Rprecision due to their high correlation with the high-cost precision metric on the data set. For each of these metrics, topic and system scores were computed at the cut-off depths ranging from ten to thirty using the trec_eval package from TREC and the rank biased precision package from the authors. Also, the high-cost precision metric was computed at the cut-off depths of 100, 500 and 1000. Table 2 below shows the information retrieval evaluation metrics and the cut-off depths at which they were computed.
| No. | Metric | Formula | Reference | Depth |
|---|---|---|---|---|
| 1 | Precision(P) | (Manning et al., 2008) | 10,15,20,25,30, 100, 500, 1000 | |
| 2 | Rank biased precision (RBP) | (Moffat and Zobel, 2008) | 10,15,20,25,30 | |
| 3 | Expected reciprocal rank(ERR) | (Chapelle et al., 2009) | 10,15,20,25,30 | |
| 4 | Non-cumulative discounted gain (nDCG) | (Järvelin and Kekäläinen, 2002) | 10,15,20,25,30 | |
| 5 | Inferred average precision (infAP) | (Yilmaz and Aslam, 2006) | 10,15,20,25,30 | |
| 6 | RPrecision | (Manning et al., 2008) | 10,15,20,25,30 | |
| 7 | Fmeasure | 10,15,20,25,30 | ||
| 8 | Recall | (Manning et al., 2008) | 10,15,20,25,30 | |
| 9 | Binary preference (bpref) | (Buckley and Voorhees, 2004) | 10,15,20,25,30 |
Generation of training and test sets
After the computation of evaluation metrics for the chosen TREC runs, topic and system data sets were generated comprising of topic and system scores respectively. Training data sets comprised topic and system scores computed from TREC 2000, 2001 and 2004 data. Test data sets comprised topic and system scores computed from TREC 2012 and 2013 data. Topic data sets were used with the proposed method. Similar to previous research, the system data sets were used with the baseline method. The procedure for generating the topic and system data sets included segmentation of data by TREC tracks, data cleaning which involved the removal of duplicate runs and suspicious zero values in the generated data sets. Table 3 below lists the features and TREC tracks used for generating the training and test sets.
| Features | Trec | Dataset type |
|---|---|---|
| ERR@10, P@10, P@100, P@500, P@1000, nDCG@10, infAP@10, RBP@10, bpref@10, R@10, Rprec@10, F-Measure@10, ERR@15, P@15, nDCG@15, infAP@15, RBP@15, bpref@15, R@15, Rprec@15, F-Measure@15, ERR@20, P@20, nDCG@20, infAP@20, RBP@20, bpref@20, R@20, Rprec@20, F-Measure@20, ERR@25, P@25, nDCG@25, infAP@25, RBP@25, bpref@25, R@25, Rprec@25, F-Measure@25, ERR@30, P@30, nDCG@30, infAP@30, RBP@30, bpref@30, R@30, Rprec@30, F-Measure@30 | TREC 2000 - Web Track, TREC 2001 - Web Track, TREC 2004 - Robust Track | Training |
| TREC 2012 - Web Track | Test - 2012 | |
| TREC 2013 - Web Track | Test - 2013 |
Node analysis
In this phase, an initial deep learning model was created and a grid search was performed to find the number of nodes at which it performed best. This was performed at each of the cut-off depths for features ranging from ten to thirty and the high-cost precision metric with cut-off depths of 100, 500 and 1000 respectively. The findings were that at eleven nodes, the model generated the least mean square error for each depth, hence its choice for the method. The mean square error is an average difference between the expected and the actual values of the target variable in the data set.
Layer analysis
In this phase, using the initial deep learning model with eleven nodes, a grid search was performed to find the number of layers at which the deep learning model performed best. This was performed at each of the cut-off depths for features ranging from ten to thirty and the high-cost precision metric with cut-off depths of 100, 500 and 1000 respectively. The findings were that from nine hidden layers onwards, the least mean square error was observed for each depth, hence it's choice for the proposed method.
Ensemble analysis
In this phase, using the initial deep learning model with eleven nodes and nine hidden layers, a grid search was performed to find the number of models to form a stacked generalization deep learning ensemble that could predict the high-cost precision metric with least mean square error. It was found that with the increase in the number of models in the ensemble, the mean square error kept reducing and with five models in the ensemble, the mean square error was least compared to ensembles comprised of fewer models. For ensembles with more than five models, small performance differences were observed when compared with ensemble with five models. Therefore, five models in the ensemble were chosen to be used at every depth of high-cost precision metric prediction.
Method build
Using the findings of the node, layer and ensemble analysis described in the previous subsections, a method was developed that employs the deep learning ensemble to predict the high-cost precision metric at the cut-off depths of 100, 500 and 1000 respectively using other metrics as features computed at depths ranging from 10 to 30. The flowchart showing steps for the proposed method is shown in Figure 1 below.
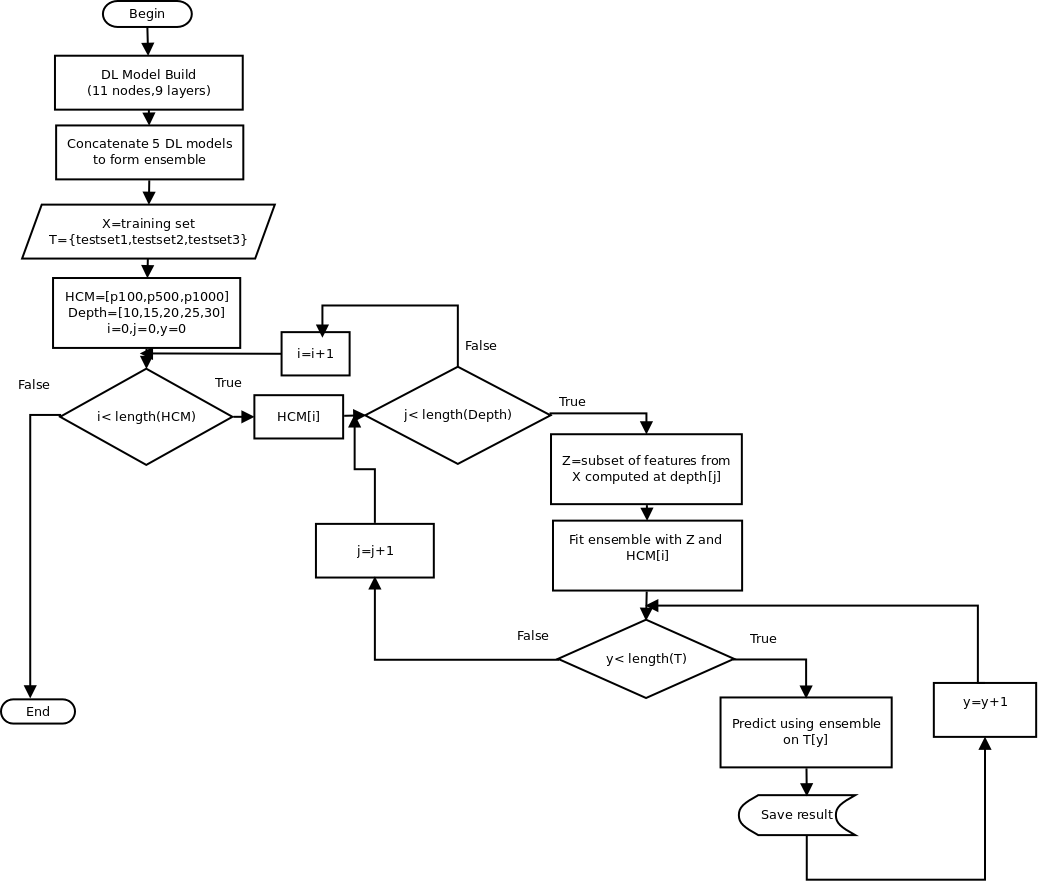
Note: T represents a list of test datasets. HCM represents the list of high-cost metrics that were being predicted. p100 means precision@100,p500 means precision@500 and p1000 means precision@1000. Depth represents cut-off depths at which features were computed. Z represents subsets of features based on the depths at which they were being computed. X represents the training dataset and variables i, j and y were used in the various iterations in the proposed method.
In this method, the stacked generalization deep learning ensemble is fit with subsets of features that were computed at depths ranging from ten to thirty documents. For each of the cut-off depths, the method predicts the high-cost precision metric at depths of 100, 500 and 1000 respectively. Using these predicted values, correlation coefficients and coefficient of determination listed below were computed for all the test cases.
Performance evaluation
The Kendall's tau, Spearman correlations, and coefficient of determination were chosen for performance evaluation of the proposed method. Similar to previous research, the correlation coefficients were used to measure the correlations in rankings based on the predicted scores. The coefficient of determination was used to measure the accuracy of the predicted scores of the high-cost precision metrics. Results are presented in Figures 2 to 4, and Tables 6 to 8. In addition, the difference in the performance between the proposed and baseline methods have been computed using the following proposed equation definitions (1) and (2) below:
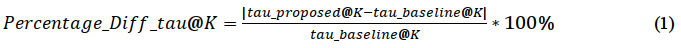
Where Percentage_Diff_tau@k is the percent difference between the Kendall’s tau ranked correlations of the predictions of the proposed and the baseline methods. The tau_proposed@k is the Kendall’s tau ranked correlation of the prediction of the proposed method and tau_baseline is the Kendall’s tau ranked correlation of the prediction of the baseline method. k is the cut-off depth of low-cost evaluation metrics.
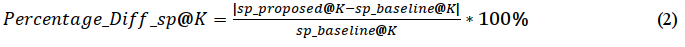
Where Percentage_Diff_sp@k is the percent difference between the Spearman ranked correlations of the predictions of the proposed and the baseline methods. The sp_proposed@k is the Spearman ranked correlation of the prediction of the proposed method and sp_baseline@k is the Spearman ranked correlation of the prediction of the baseline method. k is the cut-off depth of low-cost evaluation metrics.
Results and discussion
This section presents the results and discusses the mathematical intuitions for the correlations of information retrieval evaluation metrics and the proposed method that predicts the high-cost information retrieval evaluation precision metric at the cut-off depths of 100, 500 and 1000. The results of the proposed method are compared with those for the baseline method proposed by Gupta et al. (2019).
Results for the correlations of information retrieval evaluation metrics
This section presents the results of the correlations of the information retrieval evaluation metrics and begins with the mathematical intuition showing why the correlation exists between the precision and the rank biased precision evaluation metrics.
Precision and rank biased precision
Gupta et al. (2019) showed that precision@10 and precision@20 are mostly correlated with rank biased precision. We present a mathematical intuition that shows why there is a correlation between precision and rank biased precision. To explain the correlation further, the Pearson correlation of the metrics is highlighted using TREC 2000 data. For this intuition, it is assumed that the relevance score is binary and both the precision and the rank biased precision metrics have correlations investigated at similar depths.
Given the precision metric P, at the cut-off depth of k, defined as:

Where ri is the relevance score of the i-th document retrieved as ri . The relevance score ri=1 for a relevant document and ri=0 for a non-relevant document.
Now, for a rank biased precision evaluated at similar depth on the same system with parameter p, we have from its definition as:

Where ri is the relevance score of the i-th document retrieved as ri. The relevance score ri=1 for a relevant document and ri=0 for a non-relevant document. In addition, p the persistent parameter shows the probability that user’s progress from one document to the next in the ranked list. Hence, users end examination of a ranked list with probability (1-p).
We now analyse the correlation between P@k and RBP@k when the parameter p->1 (i.e., a very high value of p).
Suppose in equation (4) p ->1 ⇒ (1-p) ≈ a and p(i-1)≈1 for all i,
Since p is a constant and p-> 1, let a =(1-p)be a small constant.


Since p(i-1) ≈ 1 and (1-p) ≈ a We have,

The outcome a ⁄ k is a constant. This implies that P@k and RBP@k are linearly related, which thereby implies that the two metrics have a Pearson Correlation Coefficient of 1, which indicates a very high correlation. Also, note that for a given p, as k increases to large values, the approximation p(i-1) ≈ 1 becomes less and less appropriate. Therefore, for a given p, the correlation is higher at lower depths. Hence, the above mathematical procedure provides a good intuition as to why RBP@k and P@k have high correlations at higher values of p and lower values of k.
| Depth | Rank Biased Precision Persistent Parameter, P | ||||
|---|---|---|---|---|---|
| 0.7 | 0.8 | 0.85 | 0.90 | 0.95 | |
| 10 | 0.910846 | 0.954662 | 0.972629 | 0.986353 | 0.995012 |
| 20 | 0.833040 | 0.898998 | 0.934242 | 0.966631 | 0.990122 |
| 30 | 0.786663 | 0.856523 | 0.898464 | 0.943204 | 0.982329 |
| 50 | 0.720361 | 0.791231 | 0.837232 | 0.894192 | 0.960719 |
| 100 | 0.632424 | 0.702202 | 0.749689 | 0.813191 | 0.907332 |
| 1000 | 0.484015 | 0.547582 | 0.592417 | 0.655291 | 0.758912 |
Table 4 presents Pearson correlation values for the precision and rank biased precision metrics. The cut-off depths at which the metrics were computed range from ten to 1000 and the persistent parameter for the rank biased precision range from 0.7 to 0.95. Since the persistent parameter is a probability, its value lies between 0 and 1. It is clear from these Pearson correlation values, that as the persistent parameter approaches 1, there is higher Pearson correlation between P and RBP, which is in line with the intuition presented in this subsection.
Recall and average precision
The investigation of the correlation between average precision and recall showed that the correlation between these two metrics decreases as the depth of evaluation increases. A mathematical explanation to give the same intuition to the reader is presented. Consider a similar system of binary relevance evaluated at depth k, where the relevance score of the i-th document retrieved is denoted by ri
Given the average precision metric at the cut-off depth of k defined as:

and the recall metric also at the cut-off depth of k defined as:

First, let us consider the case when the evaluation depth k = 1. Then,

Similarly,

Clearly, AP@1=Recall@1 (independent of the retrieval system used).
This constant linear relationship between AP@1 and Recall@1 implies a very high Pearson correlation coefficient of 1 at k=1.
Now, consider the case when k =2. Here:

And

It is clear from equations (11) and (12) that the two evaluation metrics deviate from their linear relationship, and the relationship becomes dependent on the relevance of the documents retrieved by each system.
Suppose we calculate the correlation between AP and Recall using the performance of N systems. The correlation is always 1 for depth k=1. This is because at k=1 if a system s1 has Recall@1=0, the AP@1 will also be equal to 0. Similarly, if a system s2 has Recall@1 = (1/R), the AP@1 will also be equal to (1/R). The set of points of the ordered pair (Recall, AP) obtained can be {(0,0), (1/R, 1/R)} which satisfy a linear relationship, indicate a very high correlation of 1.
Now for k=2, the set of possible points of the ordered pair (Recall, AP) becomes {(0, 0), (1/R, 1/R), (1/R, 1/2R), (2/R, 3/2R)}. Clearly, a strictly linear relationship is possible only if all of the N systems happen to be producing at most 2 of the above possible set of points, the probability for which is clearly less than the previous case (k=1).
With an increase in the value of n, the expressions involve a greater number of dependence on the actual documents retrieved by the system which leads to greater variability in the association between the two metrics. Therefore, the probabilistic possibility of a linear dependence between the data plotted for Recall and AP decreases further and further. This explanation gives an intuition as to why the Pearson correlation between Recall and AP decreases with the increase in the evaluation depth k.
| n | 10 | 20 | 30 | 50 | 100 | 1000 |
|---|---|---|---|---|---|---|
| Correlation r | 0.903613 | 0.870689 | 0.852809 | 0.825346 | 0.777086 | 0.617946 |
Table 5 presents the Pearson correlation values for the recall and average precision metrics. The cut-off depths at which the metrics were computed range from ten to 1000. The strongest correlation is observed at lower cut-off depths. This is easily explained using the presented intuition above. It was shown above that at rank 1, the correlation was strongest (i.e., equal to 1) since the two metrics had the same values. However, starting from rank 2, different expressions are added to the two metrics during computations and this leads to drifts between them. Also, it was shown that at rank 2, to average precision is added r2/2 and to recall is added r2. As the cut-off depth increases, the more the expressions are added and the lower, the correlation becomes between the two metrics. That is why for instance at rank 10 in Table 5, there is a higher correlation (0.903613) than all ranks greater than 10.
Results for the effect of the distributions of relevance assessments on the correlations of the information retrieval evaluation metrics
This section presents the results of the effect of the variations of relevance assessments on the Pearson correlations of the precision and the rank biased precision evaluation metrics as well as the Pearson correlations of the recall and the average precision evaluation metrics.
Figure 2 below shows the results of the Pearson correlations of the rank biased precision, precision, recall and average precision evaluation metrics using samples of topic scores with varied proportions of relevance assessments computed using TREC 2000 Web Track. As seen from Figure 2, there are two samples of topic scores used. Sample 1 comprises topic scores of the evaluation metrics and topics with varied relevance assessments such that between 0 and 50 per cent of the returned documents in the represented runs per topic were not present in the query relevance file of the test collection. while Sample 2 comprises topic scores of the evaluation metrics and topics with varied relevance assessments such that between 50 and 100 per cent of the returned documents in the represented runs per topic were not present in the query relevance file of the test collection. This means that Sample 1 comprises topic scores computed using more relevance assessments from the query relevance file than Sample 2.
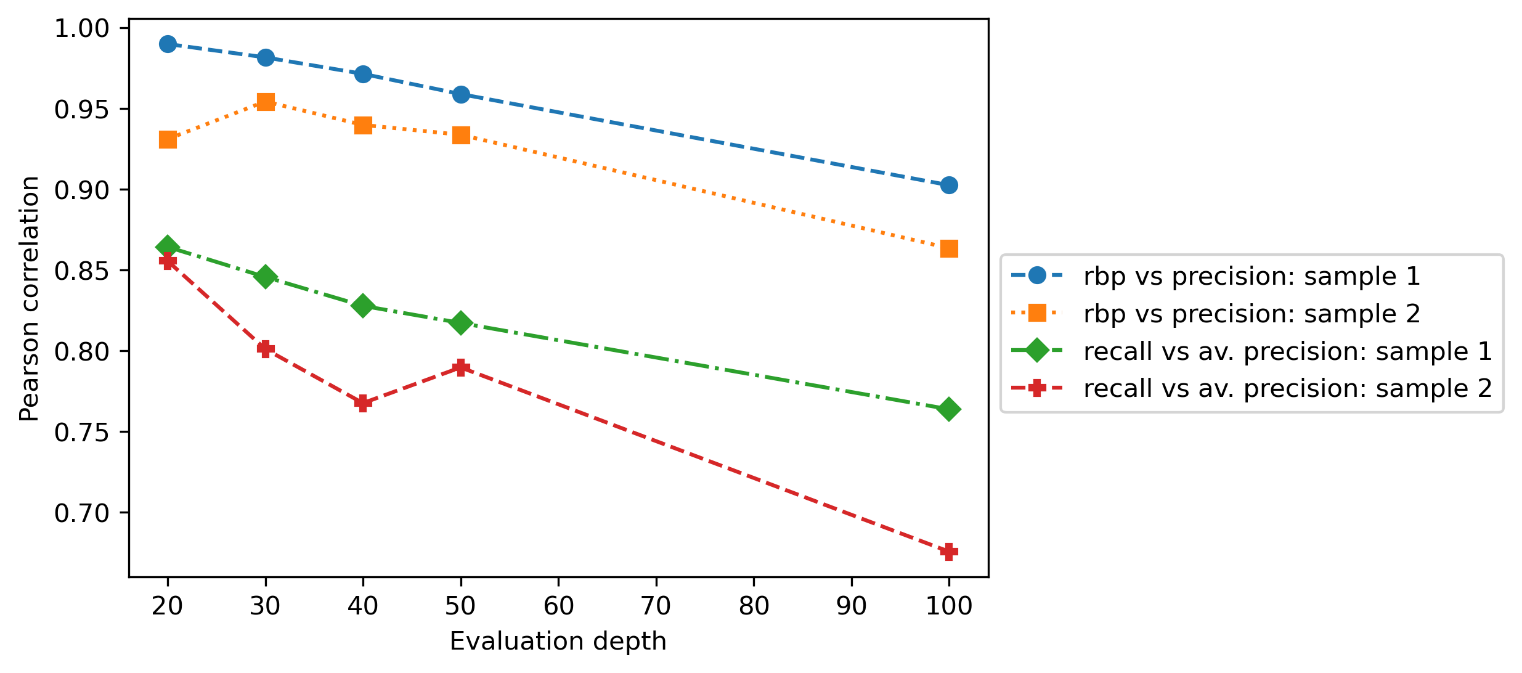
Concerning the rank biased precision and precision pair of evaluation metrics, the result shows that the Pearson correlation computed using Sample 1 was higher than the Pearson correlation computed using Sample 2 on all the evaluation depths of documents. For instance, at the evaluation depth of twenty documents, the Pearson correlation using Sample 1(0.9898) was higher than the Pearson correlation using Sample 2(0.9309) by 5.32 per cent.
Regarding the recall and average precision pair of evaluation metrics, the result also shows that the Pearson correlation computed using Sample 1 was better than the Pearson correlation computed using Sample 2 on all the evaluation depths of documents. For instance, at the evaluation depth of 100 documents, the Pearson correlation using Sample 1(0.7637) was better than the Pearson correlation using Sample 2(0.6756) by 8.81 per cent.
The above result leads us to conclude that when there are more relevance assessments in the sample of topic scores of evaluations metrics, the Pearson correlation values in the experiments tend to be higher in the case of the evaluation depths of up to 100 documents. Further, the result validates the presented mathematical intuitions in that the Pearson correlation results for both pairs of evaluation metrics on the two samples shows the similar trend as observed in Tables 1 and 2 where the Pearson correlations tend to be higher at the lower evaluation depths but tend to gradually decrease towards the higher evaluation depths of documents.
Results for the prediction of the high-cost precision metric
We present here the results and discussion of the prediction of the high-cost precision metric at the cut-off depths of 100, 500 and 1000. The cut-off depths at which the features (low-cost metrics) were computed ranged from ten to thirty. The Kendall's tau and Spearman correlation results are presented first, followed by the coefficient of determination. Further, the results obtained by the proposed method are compared with those for the baseline method proposed by Gupta et al. (2019). The training dataset was generated from TREC 2000 and TREC 2001 Web tracks, as well as TREC 2004 robust track. In addition, the test data sets were generated from TREC 2012 and TREC 2013 Web tracks.
Results for the prediction of precision@1000
Figure 3 presents Kendall's tau and Spearman correlations of both proposed and baseline methods for the prediction of precision@1000. The other metrics, which were features, were computed at the cut-off depths ranging from ten to thirty.
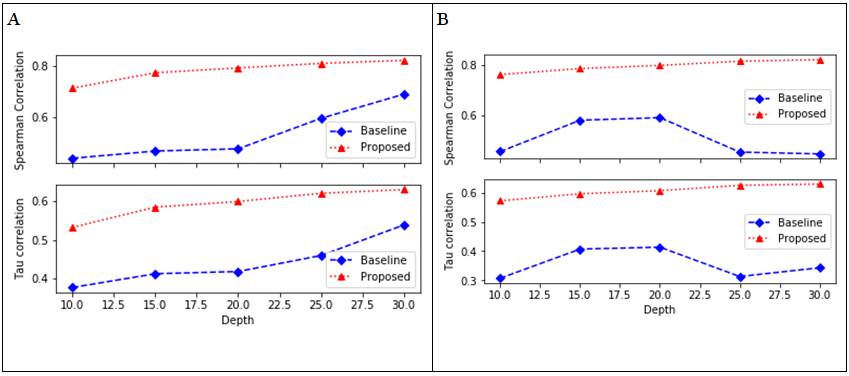
Note: A test data were from TREC 2012 and B test data were from TREC 2013.
Figure 3 illustrates the results of Kendall's tau and Spearman correlations of both baseline and proposed methods for the prediction of precision@1000 using the test datasets generated from TREC 2012 and TREC 2013 data. Figure 3(A) shows results when TREC 2012 data is used, while fig. 3(B) shows results when TREC 2013 data is used. In both cases, features were computed at the cut-off depths ranging from ten to thirty.
In Figure 3(A), the result shows that the proposed method had better performance than its baseline on all the cut-off depths at which features were computed because of its higher Kendall's tau and Spearman correlations. Using the results shown in Figure 3 above, the extent to which the proposed method performed better than the baseline concerning the Kendall’s tau and Spearman ranked correlations was computed using equations (1) and (2) respectively. For instance, at the cut-off depth of twenty-five, the proposed method’s Kendall's tau and Spearman correlation values were higher by 35.0 per cent and 36.2 per cent respectively. At the cut-off depth of thirty, the proposed method’s Kendall's tau (0.63020) and Spearman (0.822030) correlations were higher than the baseline by 17.0 per cent and 19.3 per cent respectively. A similar trend can be seen from Figure 3 (B), where the proposed method also performed better than its baseline on all the depths of features because of its superior Kendall's tau and Spearman correlations. When compared to its baseline at the depth of twenty, the proposed method’s Kendall's tau and Spearman correlation values were higher by 46.4 per cent and 34.7 per cent respectively.
Table 6 shows the values of the coefficient of determination following the prediction of precision@1000 by the proposed and the baseline methods using test data sets generated from TREC 2012 and TREC 2013 Web track data.
| Method | Depth | R-Squared-TREC 2012 | R-Squared-TREC 2013 |
|---|---|---|---|
| Baseline | 10 | -1.187400 | -1.342262 |
| 15 | -1.052810 | -0.751991 | |
| 20 | -0.916083 | -0.538088 | |
| 25 | -0.564947 | -1.952770 | |
| 30 | -0.194158 | 0.065768 | |
| Proposed | 10 | -0.202506 | 0.266719 |
| 15 | -0.207175 | 0.216056 | |
| 20 | -0.370490 | -0.018994 | |
| 25 | -0.369697 | 0.107549 | |
| 30 | -0.184796 | 0.275984 |
A close inspection of the results shown in Table 6 highlights the supremacy of the predictive accuracy of the proposed method over the baseline method on most of the cut-off depths at which features were computed. For instance, at the cut-off depth of features of thirty for TREC 2012 data, the coefficient of determination for the proposed method was higher than the baseline method by above 4.8 per cent. Further, the results also show that as the cut-off depth of at which features were computed increases, the coefficient of determination for both methods increases.
Results for prediction of precision@500
Figure 4 shows Kendall’s tau and Spearman correlations of both proposed and baseline methods for the prediction of precision@500. The other metrics that were features were computed at the cut-off depths ranging from ten to thirty.
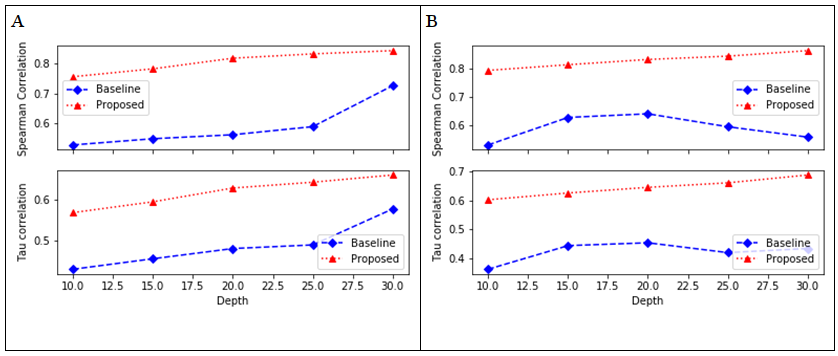
Note: A test data were from TREC 2012 and B test data were from TREC 2013.
Figure 4 provides the results of Kendall’s tau and Spearman correlations of both proposed and baseline methods for the prediction of precision@500 using the test data sets generated from TREC 2012 and TREC 2013 data. Figure 4(A) shows results when TREC 2012 data is used, while Figure 4(B) shows results when TREC 2013 data is used. In both cases, features were computed at the cut-off depths ranging from ten to thirty. It is clear from Figure 4(A), that the proposed method is better than its baseline on all the cut-off depths of features due to its higher Kendall’s tau and Spearman correlations. For example, at the cut-off depth of thirty, the proposed method’s Kendall’s tau and Spearman correlation values were higher by 14.6 per cent and 16.2 per cent respectively. Furthermore, it is apparent from Figure 4(B) that the proposed method also performed better than its baseline on all the depths of features due to its superior Kendall’s tau and Spearman correlations. When compared to its baseline at the depth of twenty, the proposed method’s Kendall’s tau and Spearman correlation values were higher by 42.4 per cent and 29.9 per cent respectively. Table 7 provides the values of the coefficient of determination following the prediction of precision@500 by the proposed and the baseline methods using test data sets generated from TREC 2012 and TREC 2013 Web track data.
| Method | Depth | R-Squared-TREC 2012 | R-Squared-TREC 2013 |
|---|---|---|---|
| Baseline | 10 | -0.423433 | -0.364781 |
| 15 | -0.322298 | -0.036684 | |
| 20 | -0.241708 | 0.105773 | |
| 25 | 0.033048 | 0.269949 | |
| 30 | 0.183039 | 0.342159 | |
| Proposed | 10 | 0.095055 | 0.385867 |
| 15 | -0.054908 | 0.273776 | |
| 20 | -0.107077 | 0.153814 | |
| 25 | -0.172268 | 0.234604 | |
| 30 | 0.012593 | 0.402813 |
A look at the results displayed in Table 7 shows the supremacy of the predictive accuracy of the proposed method over the baseline method on most of the cut-off depth of features. For instance, at the cut-off depth of features of thirty for TREC2013 data, the coefficient of determination for the proposed method was higher than the baseline method by 17.7 per cent. The same trend is observed on TREC 2012 where the cut-off depth is less than 25. Further, the results show that as the cut-off depth of features increases, the coefficient of determination for both methods increases. Comparing data in this table with Table 6 reveals that the greater the cut-off depth of the predicted high-cost precision metric, the less the predictive accuracy of the method. In addition, for both methods, the predictive accuracy increases with the increase in the cut-off depth at which the features were computed, though decreases with the increase in the cut-off depth of the high-cost precision metric.
Results for prediction of precision@100
Figure 5 presents Kendall's tau and Spearman correlations of both proposed and baseline methods for the prediction of precision@100. The other metrics that were features were computed at the cut-off depths ranging from ten to thirty.
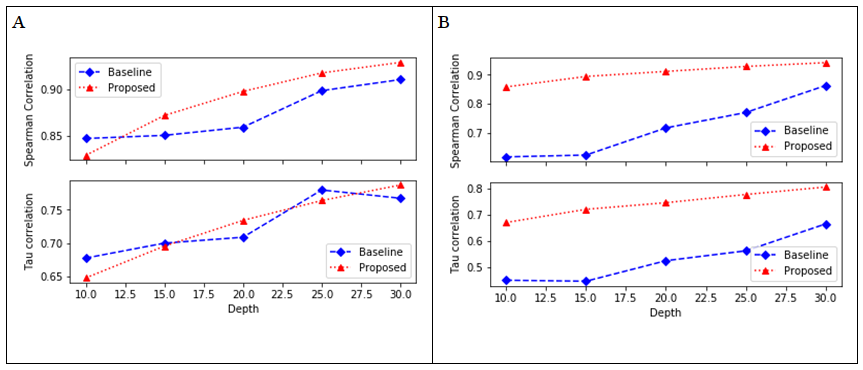
Note: A test data were from TREC 2012 and B test data were from TREC 2013.
Figure 5 provides the results of Kendall's tau and Spearman correlations of both proposed and baseline methods for the prediction of precision@100 using the test data sets generated from TREC 2012 and TREC 2013 data. Figure 5(A) shows results when TREC 2012 data is used, while Figure 5(B) shows results when TREC 2013 data is used. In both cases, features were computed at the cut-off depths ranging from ten to thirty. In Figure 5(B), the result shows that the proposed method is superior over its baseline on all the cut-off depths of features because of its higher Kendall's tau and Spearman correlations. For instance, at the cut-off depth of thirty, the proposed method’s Kendall's tau (0.8049) and Spearman (0.9416) correlations were higher than the baseline by 21.0 per cent and 9.1 per cent respectively. Also, as can be seen from Figure 5(A), the proposed method performed better than its baseline on the cut-off depth of thirty and twenty on TREC 2012 data. Table 8 presents the values of the coefficient of determination following the prediction of precision@100 by the proposed and the baseline methods using test data sets generated from TREC 2012 and TREC 2013 Web track data.
| Method | Depth | R-Squared-TREC 2012 | R-Squared-TREC 2013 |
|---|---|---|---|
| Baseline | 10 | 0.725232 | 0.364191 |
| 15 | 0.627067 | 0.524858 | |
| 20 | 0.682360 | 0.594896 | |
| 25 | 0.730939 | 0.669583 | |
| 30 | 0.804948 | 0.722241 | |
| Proposed | 10 | 0.562821 | 0.551175 |
| 15 | 0.631095 | 0.648645 | |
| 20 | 0.638844 | 0.689969 | |
| 25 | 0.647587 | 0.714961 | |
| 30 | 0.697310 | 0.797089 |
In Table 8, it is apparent that the predictive accuracy of the proposed method is higher than the baseline due to the higher coefficient of determination on the data set generated from TREC 2013 data. At the cut-off depth of ten of features, the result shows that the coefficient of determination for the proposed method (0.551175) was higher than the one for the baseline method (0.364191) for TREC2013. Nevertheless, the baseline method performed well on several cut-off depths at which features were computed on TREC 2012 data.
In summary, comparing results shown in figures and tables above, it is clear that the greater the cut-off depth of the high-cost precision metric being predicted, the less the predictive accuracy of the proposed and baseline methods. Also, for both methods, the predictive accuracy increases with the increase in the cut-off depth at which the features were computed, though decreases with the increase in the cut-off depth of the high-cost precision metric. This confirms the results of the research by Gupta et al. (2019).
Conclusion
As a way of reducing costs in information retrieval evaluation, this study has proposed a method to predict the high-cost precision evaluation metrics at the cut-off depths of 100, 500 and 1000 using other evaluation metrics computed at the lower cut-off depths ranging from ten to thirty documents. In addition, the proposed method employs the stacked generalization deep learning ensemble and has shown to be better than the baseline method on all the cut-off depths of documents for the predicted high-cost precision metric. Furthermore, the justifications through mathematical intuitions have been presented for the correlation of the precision and rank biased precision metrics and also why recall and average precision have reduced correlation when the cut-off depth increases.
We also investigated the effect of the variations of relevance assessments on the correlations of the evaluation. Despite the achievements in this study, there is still room for future work. Many correlations between information retrieval evaluation metrics have been identified in previous research (Baccini et al., 2012; Gupta et al., 2019; Tague-Sutcliffe and Blustein, 1995). However, justifications for most of these correlations are lacking. Furthermore, the proposed method for the prediction of the high-cost precision metrics could be further enhanced in order to improve its predictive accuracy especially for the higher cut-off depths of the high-cost precision metric such as 500 and 1000 documents. In addition, there is a need to investigate the effect of contributing and non-contributing systems in the TREC tracks on the predictions of high-cost evaluation metrics. Lastly, the selection of a specific number of topic scores could be attempted in the process of creating the training set and an investigation could be carried out to ascertain the extent to which prediction of high-cost metrics is influenced.
Acknowledgements
This research work has been supported by the University of Malaya RU Grant GPF001D-2018 and the University of Malaya Interdisciplinary Research Grant Programme IIRG005B-2020SAH by Ministry of Higher Education, Malaysia.
About the authors
Sinyinda Muwanei received his BSc and MSc degrees in Engineering and Technology specializing in Systems Analysis and Control from Saint Petersburg State Polytechnical University, Russia, and Master of Business Administration from Amity University, India. He is a PhD candidate at the University of Malaya in Malaysia. His research interests include information retrieval, distributed systems and artificial intelligence. He can be contacted at: smuwanei@gmail.com
Sri Devi Ravana received her Ph.D from The University of Melbourne, Australia, in 2012. She is currently an Associate Professor at the Department of Information Systems, University of Malaya. Her research interests include information retrieval heuristics, text indexing and data analytics. She can be contacted at: sdevi@um.edu.my
Wai Lam Hoo is currently a senior lecturer in Department of Information Systems, Faculty of Computer Science and Information Technology, University of Malaya, Malaysia. He obtained his Ph.D in the same university, and his research interest includes computer vision, machine learning and data analytics. He can be contacted at: wlhoo@um.edu.my
Douglas Kunda is an Associate Professor in Software Engineering and founding Dean of the School of Science, Engineering and Technology, Mulungushi University, Zambia. He obtained his Ph.D in Computer Science from the University of York, UK. His research interest includes software engineering, artificial intelligence, component-based software engineering, internet of things, machine learning and data mining. He can be contacted at: dkunda@mu.ac.zm
Prabha Rajagopal is an academic at the School of Information Technology (SoIT), Monash University, Malaysia. She received her BEng (Hons) in Electronics from Multimedia University, Malaysia. She obtained her Master of Computer Science in 2014 and Doctor of Philosophy (PhD) in Computer Science in 2018, both from the University of Malaya. Her research interests are information retrieval, machine learning and data analytics. She can be contacted at: prabz13@yahoo.com
Prabhpreet Singh Sodhi is a Computer Science graduate from Indian Institute of Technology, Kharagpur, India. He interned at the Faculty of Computer Science and Information Technology, University of Malaya in the summer of 2019. His areas of interest are computer systems, information retrieval and decentralised robotics. He can be contacted at: pprabh2007@gmail.com
References
Note: A link from the title, or from "(Internet Archive)", is to an open access document. A link from the DOI is to the publisher's page for the document.
- Aslam, J. A., & Yilmaz, E. (2007). Inferring document relevance from incomplete information. In CIKM ’07: Proceedings of the Sixteenth ACM Conference on Conference on Information and Knowledge Management (pp. 633–642). https://doi.org/10.1145/1321440.1321529
- Aslam, J. A., Yilmaz, E., & Pavlu, V. (2005). A geometric interpretation of r-precision and its correlation with average precision. In SIGIR ’05:Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (pp. 573-5740). https://doi.org/10.1145/1076034.1076134
- Baccini, A., Déjean, S., Lafage, L., & Mothe, J. (2012). How many performance measures to evaluate information retrieval systems? Knowledge and Information Systems, 30(3), 693–713. https://doi.org/10.1007/s10115-011-0391-7
- Berto, A., Mizzaro, S., & Robertson, S. (2013). On using fewer topics in information retrieval evaluations. In ICTIR '13: Proceedings of the 2013 Conference on the Theory of Information Retrieval, Copenhagen, Denmark, 29 September 2013-2 October 2013 (pp. 30–37). Association for Computing Machinery. https://doi.org/10.1145/2499178.2499184
- Buckley, C., & Voorhees, E. M. (2004). Retrieval evaluation with incomplete information. In SIGIR ’04: Proceedings of the 27th Annual International ACM Conference on Research and Development in Information Retrieval, Sheffield, United Kingdom, July 25-29, 2004 (pp. 25–32). Association for Computing Machinery. https://doi.org/10.1145/1008992.1009000
- Büttcher, S., Clarke, C. L. A., Yeung, P. C. K., & Soboroff, I. (2007). Reliable information retrieval evaluation with incomplete and biased judgements. In SIGIR ’07: Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Amsterdam The Netherlands July 23 - 27, 2007 (pp. 63–70). Association for Computing Machinery. https://doi.org/10.1145/1277741.1277755
- Carterette, B., & Allan, J. (2005). Incremental test collections. In CIKM’05: Proceedings of the 14th International Conference on Information and Knowledge Management, Toronto ON Canada October 26 - 30, 2010 (pp. 680–687). Association for Computing Machinery. https://doi.org/10.1145/1871437.1871568
- Carterette, B., Allan, J., & Sitaraman, R. (2006). Minimal test collections for retrieval evaluation. In SIGR’06: Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Seattle, Washington, USA, August 6-11, 2006 (pp. 268–275). Association for Computing Machinery. https://doi.org/10.1145/1148170.1148219
- Carterette, B., Pavlu, V., Kanoulas, E., Aslam, J. A., & Allan, J. (2008). Evaluation over thousands of queries. In SIGIR ‘08” Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval Singapore, July 20 - 24, 2008 (pp. 651–658). Association for Computing Machinery. https://doi.org/10.1145/1390334.1390445
- Chapelle, O., Metlzer, D., Zhang, Y., & Grinspan, P. (2009). Expected reciprocal rank for graded relevance. In CIKM ’09: Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, November 2-6, 2009 (pp. 621–630). Association for Computing Machinery. https://doi.org/10.1145/1645953.1646033
- Clarke, C. L. A., Craswell, N., & Voorhees, E. M. (2012). Overview of the TREC 2012 Web Track. In Proceedings of the 21st Text Retrieval Conference, TREC 2012, Gaithersburg, Maryland, (8 p.). National Institute of Standards and Technology. https://trec.nist.gov/pubs/trec21/papers/WEB12.overview.pdf (Internet Archive)
- Collins-Thompson, K., Bennett, P., Diaz, F., Clarke, C. L., & Voorhees, E. M. (2013). TREC 2013 Web Track Overview. In Proceedings of the 22nd Text Retrieval Conference, TREC 2013, Gaithersburg, Maryland, (15 p.). National Institute of Standards and Technology. http://trec.nist.gov/pubs/trec22/papers/WEB.OVERVIEW.pdf (Internet Archive)
- Cormack, G. V., Palmer, C. R., & Clarke, C. L. A. (1998). Efficient construction of large test collections. In SIGIR ’98:Proceedings of the 21st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval , Melbourne, Australia, August 24-28, 1998 (pp. 282–289). Association for Computing Machinery.https://dl.acm.org/doi/10.1145/290941.291009
- Ferro, N., Fuhr, N., Järvelin, K., Kando, N., Lippold, M., & Zobel, J. (2016). Increasing reproducibility in IR: findings from the Dagstuhl Seminar on "Reproducibility of Data-Oriented Experiments in e-Science". ACM SIGIR Forum, 50(1), 68-82.ACM. https://doi.org/10.1145/2964797.2964808
- Fuhr, N. (2018). Some common mistakes in IR evaluation, and how they can be avoided. ACM SIGIR Forum, 51(3), 32-41. https://doi.org/10.1145/3190580.3190586
- Guiver, J., Mizzaro, S., & Robertson, S. (2009). A few good topics: experiments in topic set reduction for retrieval evaluation. ACM Transactions on Information Systems, 27(4), 1–26. https://doi.org/10.1145/1629096.1629099
- Gupta, S., Kutlu, M., Khetan, V., & Lease, M. (2019). Correlation, prediction and ranking of evaluation metrics in information retrieval. In L. Azzopardi, B. Stein, N. Fuhr, P. Mayr, C. Hauff, and D. Hiemstra (Eds.). 41st European Conference on IR Research, ECIR 2019, Cologne, Germany, April 14–18, 2019, Proceedings, Part I. Springer. https://doi.org/10.1007/978-3-030-15712-8_41
- Hosseini, M., Cox, I. J., Milić-Frayling, N., Shokouhi, M., & Yilmaz, E. (2012). An uncertainty-aware query selection model for evaluation of IR systems. In SIGIR ’12: Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval (pp. 901–910). https://doi.org/10.1145/2348283.2348403
- Hosseini, M., Cox, I. J., Milic-Frayling, N., Sweeting, T., & Vinay, V. (2011). Prioritizing relevance judgments to improve the construction of IR test collections. In CIKM ’11: Proceedings of the 20th ACM International Conference on Information and Knowledge Management Portland, Oregon, USA, August 12-16, 2012(pp. 641–646). Association for Computing Machinery. https://doi.org/10.1145/2063576.2063671
- Järvelin, K., & Kekäläinen, J. (2002). Cumulated gain-based evaluation of IR techniques. ACM Transactions on Information Systems, 20(4), 422–446. https://doi.org/10.1145/582415.582418
- Kutlu, M., Elsayed, T., & Lease, M. (2018). Intelligent topic selection for low-cost information retrieval evaluation: a new perspective on deep vs. shallow judging. Information Processing and Management, 54(1), 37–59. https://doi.org/10.1016/j.ipm.2017.09.002
- Losada, D. E., Parapar, J., & Barreiro, A. (2017). Multi-armed bandits for adjudicating documents in pooling-based evaluation of information retrieval systems. Information Processing and Management, 53(5), 1005–1025. https://doi.org/10.1016/j.ipm.2017.04.005
- Makary, M., Oakes, M., Mitkov, R, & Yammout, F. (2017). Using supervised machine learning to automatically build relevance judgments for a test collection. In Tjoa, A.M., & Wagner, R.R. (Eds.). Proceedings of the International Workshop on Database and Expert Systems Applications (DEXA) Lyon, France, 28-31 Aug. 2017 (pp. 108–112). Conference Publishing Services. https://doi.org/10.1109/DEXA.2017.38
- Manning, C., Raghavan, P., & Schutze, H. (2008). Introduction to information retrieval. Cambridge University Press.
- Mizzaro, S. (2008). The good, the bad, the difficult, and the easy: something wrong with information retrieval evaluation? In C. Macdonald, I. Ounis, V. Plachouras, I. Ruthven, and R. W. White (Eds.), 30th European Conference on IR Research, ECIR 2008, Glasgow, UK (pp. 642-646). Springer.
- Moffat, A., Webber, W., & Zobel, J. (2007). Strategic system comparisons via targeted relevance judgments. In SIGIR ’07: Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (pp. 375-382). Association for Computing Machinery. https://doi.org/10.1145/1277741.1277806
- Moffat, A., & Zobel, J. (2008). Rank-biased precision for measurement of retrieval effectiveness. ACM Transactions on Information Systems, 27(1), 1–27. https://doi.org/10.1145/1416950.1416952
- Moghadasi, S. I., Ravana, S. D., & Raman, S. N. (2013). Low-cost evaluation techniques for information retrieval systems: a review. Journal of Informetrics, 7(2), 301–312. https://doi.org/10.1016/J.JOI.2012.12.001
- Muwanei, S. (2021). Correlation and prediction of performance metrics in information-retrieval. GitHub repository https://github.com/smuwanei/Correlation-and-prediction-of-performance-metrics-in-information-retrieval (Internet Archive)
- Papariello, L., Bampoulidis, A., & Lupu, M. (2020). On the replicability of combining word embeddings and retrieval models. In J.M. Jose, E. Yilmaz, J. Magalhães, P. Castells, N. Ferro, M.J. Silva and F. Martins (Eds.), Advances in Information Retrieval: ECIR 2020 (pp. 50-57). Springer. (Lecture Notes in Computer Science; no. 12036). https://doi.org/10.1007/978-3-030-45442-5_7
- Rahman, M. M., Kutlu, M., & Lease, M. (2019). Constructing test collections using multi-armed bandits and active learning. In L. Liu & R. White, (Eds.). Proceedings of the World Wide Web Conference, WWW 2019, San Francisco, CA, USA, May 13 - 17, 2019 (pp. 3158–3164). Association for Computing Machinery. https://doi.org/10.1145/3308558.3313675
- Rajagopal, P., Ravana, S. D., & Ismail, M. A. (2014). Relevance judgments exclusive of human assessors in large scale information retrieval evaluation experimentation. Malaysian Journal of Computer Science, 27(2), 80–94.
- Ravana, S. D., Park, L. A., & Moffat, A. (2009). System scoring using partial prior information. In SIGIR ’08: Proceedings of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Boston, MA, USA, July 19-23, 2009 (pp. 788-789). Association for Computing Machinery. https://doi.org/10.1145/1571941.1572129
- Roitero, K., Culpepper, J. S., Sanderson, M., Scholer, F., & Mizzaro, S. (2020). Fewer topics? A million topics? Both?! On topics subsets in test collections. Information Retrieval Journal, 23(1), 49–85. https://doi.org/10.1007/s10791-019-09357-w
- Roitero, K., Passon, M., Serra, G., & Mizzaro, S. (2018). Reproduce. Generalize. Extend. On information retrieval evaluation without relevance judgments. Journal of Data and Information Quality, 10(3), article 11. https://doi.org/10.1145/3241064
- Sakai, T. (2007). On the reliability of information retrieval metrics based on graded relevance. Information Processing and Management, 43(2), 531–548. https://doi.org/10.1016/j.ipm.2006.07.020
- Sanderson, M., & Zobel, J. (2005). Information retrieval system evaluation: effort, sensitivity, and reliability. In Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Salvador, Brazil, August 15-19, 2005 (pp. 162–169). Association for Computing Machinery https://doi.org/10.1145/1076034.1076064
- Soboroff, I., Nicholas, C., & Cahan, P. (2001). Ranking retrieval systems without relevance judgments. In SIGIR ’01: Proceedings of the 24th annual international SIGIR conference on Research and Development in Information Retrieval , New Orleans, Louisiana, USA, September 9-12, 2001. (pp. 66–73). Association for Computing Machinery. https://doi.org/10.1145/383952.383961
- Tague-Sutcliffe, J., & Blustein. J. (1995). A statistical analysis of the TREC-3 Data. In D.K. Harman (Ed.), Overview of the Third Text REtrieval Conference (TREC-3). (pp. 385-398). Computer Systems Laboratory, National Institute of Standards and Technology.(NIST Special Publication 500-225).
- Thom, J. A., & Scholer, F. (2007).A comparison of evaluation measures given how users perform on search tasks. In Proceedings of the Twelfth Australasian Document Computing Symposium, December (pp. 100–103). RMIT University. (Internet Archive)
- Voorhees, E., & Harman, D. (2000). Overview of TREC-9 Web Track. In Proceedings of the 9th Text Retrieval Conference, TREC 2000, Gaithersburg, Maryland. National Institute of Standards and Technology. https://trec.nist.gov/pubs/trec9/t9_proceedings.html (Internet Archive)
- Voorhees, E., & Harman, D. (2001). Overview of the TREC-2001 Web Track. In Proceedings of the 10th Text Retrieval Conference, TREC 2001, Gaithersburg, Maryland. National Institute of Standards and Technology. https://trec.nist.gov/pubs/trec10/t10_proceedings.html (Internet Archive)
- Voorhees, E. M. (2004). Overview of the TREC 2004 Robust Track. In Proceedings of the Thirteenth Text Retrieval Conference (TREC 2004), Gaithersburg, Maryland. National Institute of Standards and Technology. https://trec.nist.gov/pubs/trec13/t13_proceedings.html (Internet Archive)
- Webber, W., Moffat, A., Zobel, J., & Sakai, T. (2008). Precision-at-ten considered redundant. In Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Singapore, July 20 - 24, 2008 (pp. 695–696). Association for Computing Machinery. https://doi.org/10.1145/1390334.1390456
- Yilmaz, E., & Aslam, J. A. (2006). Inferred AP: estimating average precision with incomplete judgments. In Proceedings of the 15th ACM International Conference on Information and Knowledge Management, (pp. 102–111). National Institute of Standards and Technology. http://trec.nist.gov/data/terabyte/06/inferredAP.pdf (Internet Archive)
- Yilmaz, E., & Aslam, J. A. (2008). Estimating average precision when judgments are incomplete. Knowledge and Information Systems, 16(2), 173–211. https://doi.org/10.1007/s10115-007-0101-7
- Zobel, J. (1998). How reliable are the results of large-scale information retrieval experiments? In SIGIR ’98: Proceedings of the 21st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Melbourne, Australia, August 24-28, 1998 (pp. 307–314). Association for Computing Machinery. https://doi.org/10.1145/290941.291014